10.03 Sine, cosine, and tangent ratios
The primary trigonometric ratios
Labeling sides
We have already seen which of the sides in a right triangle is the hypotenuse.
If we have another angle indicated (like $\theta$θ in the diagram below) then we can also label the other two sides with two special names.
Opposite Side - is the name given to the side opposite the angle in question
Adjacent Side - is the name given to the side adjacent (next to) the angle in question.
Ratio of two sides
In the right triangle below, $c$c, or $\overline{QR}$QR, is the the hypotenuse and $\angle RPQ$∠RPQ is $90^\circ$90° .
Now if we call $\angle PQR=\theta$∠PQR=θ and we can identify the opposite and adjacent sides with respect to that angle, (we did this here, if you need to refresh). So $b$b, or $\overline{PR}$PR, is the opposite side, and $a$a, or $\overline{PQ}$PQ, is the adjacent side.

Right triangle
A ratio is a statement of a mathematical relationship between two objects, often represented as a fraction. Various ratios of the following can be constructed from the right triangle with respect to angle $\theta$θ.
$\frac{Opposite}{Adjacent}=\frac{b}{a}$OppositeAdjacent=ba
$\frac{Adjacent}{Hypotenuse}=\frac{a}{c}$AdjacentHypotenuse=ac
$\frac{Opposite}{Hypotenuse}=\frac{b}{c}$OppositeHypotenuse=bc
Worked examples
Question 1
Considering the angle $\theta$θ, what is the value of the ratio $\frac{Adjacent}{Hypotenuse}$AdjacentHypotenuse ?

Think: First we need to identify which sides are the adjacent and hypotenuse with respect to angle theta. I can see that $\overline{BA}$BA is the hypotenuse side, $\overline{AC}$AC is the opposite side and $\overline{BC}$BC is the adjacent side.
Do: $\frac{Adjacent}{Hypotenuse}$AdjacentHypotenuse = $\frac{BC}{AB}=\frac{5}{13}$BCAB=513
Practice questions
Question 2
Question 3
Consider the angle $\theta$θ.
What is the value of the ratio $\frac{Opposite}{Adjacent}$OppositeAdjacent?
Express your answer as a fraction.

Sine, cosine and tangent
If we consider an angle $\theta$θ in a right triangle, the ratios we looked at above are quite important. Special relationships that exist in right triangles are called trigonometric ratios.
Through investigation we can see that there is a definite relationship between the angles in a right triangle and the ratio of sides. We can use these trigonometric ratios to find unknown angles and sides of a triangle.
There are $3$3 basic trigonometric ratios that relate sides and angles together. They have the special names of tangent, sine and cosine. The names of the relationships date back to 499AD, with ties to Latin and Sanskrit. Actually the word sine is thought to be derived from a translation gone wrong! Regardless the names for these relationships have stuck.
We often shorten the names tangent, sine and cosine to tan, sin and cos respectively.

| $\sin\theta$sinθ | $=$= | $\frac{Opposite}{Hypotenuse}$OppositeHypotenuse | $=$= | $\frac{b}{c}$bc |
| $\cos\theta$cosθ | $=$= | $\frac{Adjacent}{Hypotenuse}$AdjacentHypotenuse | $=$= | $\frac{a}{c}$ac |
| $\tan\theta$tanθ | $=$= | $\frac{Opposite}{Adjacent}$OppositeAdjacent | $=$= | $\frac{b}{a}$ba |
Here is a picture of the above relationships, and for some people the mnemonic of SOH CAH TOA at the bottom is helpful to remember the sides that apply to the different ratios of sine, cosine and tangent.
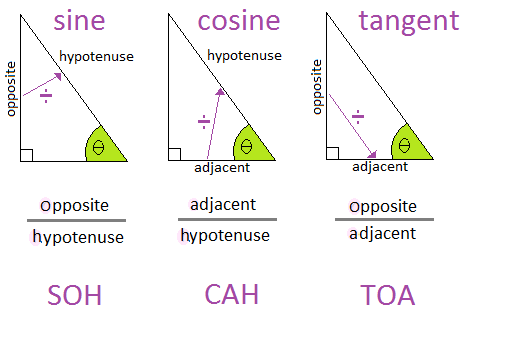
This applet will let you explore different trigonometric ratios, particularly which sides are needed for a particular ratio. If you would like to see this applet in action, watch this video.
Practice questions
Question 4
Find the value of $\tan\theta$tanθ within $\triangle ABC$△ABC.

A triangle labeled with vertices A, B, and C is shown. The angle at vertex A is labeled $\alpha$α. The angle at vertex B is labeled $\theta$θ. The angle at vertex C is a right angle as indicated by a square square. Side AB is the hypotenuse and is labeled "60," indicating its length. Side $BC$BC is labeled "20," indicating its length. Side BC is adjacent to angle $\theta$θ. Side BC is opposite angle $\alpha$α. Side AC is labeled "35," indicating its length. Side AC is adjacent to angle $\alpha$α. Side AC is opposite angle $\theta$θ.
Question 5
Consider the triangle in the figure. If $\sin\theta=\frac{4}{5}$sinθ=45:

Which angle is represented by $\theta$θ?
$\angle BAC$∠BAC
A$\angle BCA$∠BCA
B$\angle ABC$∠ABC
CFind the value of $\cos\theta$cosθ. Express your answer as a simplified fraction.
Find the value of $\tan\theta$tanθ. Express your answer as a simplified fraction.
Connection to similarity
We looked at similar triangles and learned that all the sides in similar triangles are in the same ratio. So, when we find the ratio of two sides in a triangle, the ratio of the corresponding sides in a similar triangle will always be the same.
As such, this means that the trigonometric ratios (sine, cosine and tangent) in similar right-angle triangles are always equal. Let's consider the two right triangles below.
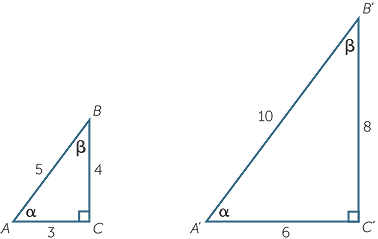
In triangle ABC:
| $\sin\alpha$sinα | $=$= | $\frac{4}{5}$45 | $\sin\beta$sinβ | $=$= | $\frac{3}{5}$35 | ||
| $\cos\alpha$cosα | $=$= | $\frac{3}{5}$35 | $\cos\beta$cosβ | $=$= | $\frac{4}{5}$45 | ||
| $\tan\alpha$tanα | $=$= | $\frac{4}{3}$43 | $\tan\beta$tanβ | $=$= | $\frac{3}{4}$34 |
In triangle A'B'C':
| $\sin\alpha$sinα | $=$= | $\frac{8}{10}$810 | $\sin\beta$sinβ | $=$= | $\frac{6}{10}$610 | ||
| $=$= | $\frac{4}{5}$45 | $=$= | $\frac{3}{5}$35 | ||||
| $\cos\alpha$cosα | $=$= | $\frac{6}{10}$610 | $\cos\beta$cosβ | $=$= | $\frac{8}{10}$810 | ||
| $=$= | $\frac{3}{5}$35 | $=$= | $\frac{4}{5}$45 | ||||
| $\tan\alpha$tanα | $=$= | $\frac{8}{6}$86 | $\tan\beta$tanβ | $=$= | $\frac{6}{8}$68 | ||
| $=$= | $\frac{4}{3}$43 | $=$= | $\frac{3}{4}$34 |
As you can see, the ratios are the same in both triangles.
So once we can prove that two triangles are similar, we can find corresponding trigonometric ratio, as well as corresponding angles and side lengths.
Practice questions
Question 6
Two right triangles are measured, and a pair of corresponding angles are found to have a sine ratio of $\frac{240}{250}$240250 and $\frac{24}{25}$2425 respectively.
Are the two triangles similar?
Yes
ANo
B
