4.07 Graphical solutions to linear equations or inequalities
Solving linear equations graphically
Typically, we think of solving linear equation as a purely algebraic process. However, there is also a graphical interpretation of solving a linear equation.
Consider the linear equation $2x+4=-6$2x+4=−6, we often look at this and immediately start solving it as below.
| $2x+4$2x+4 | $=$= | $-6$−6 |
| $2x+4-4$2x+4−4 | $=$= | $-6-4$−6−4 |
| $2x$2x | $=$= | $-10$−10 |
| $\frac{2x}{2}$2x2 | $=$= | $\frac{-10}{2}$−102 |
| $x$x | $=$= | $-5$−5 |
We want to make connections in mathematics, so let's consider the connection between solving that linear equation and graphing two lines.
Suppose I wanted to find out where the lines $y=2x+4$y=2x+4 and $y=-6$y=−6 intersect on the $xy$xy-plane.
We could first graph $y=2x+4$y=2x+4 using the slope-intercept method, shown in blue. Then graph $y=-6$y=−6 quickly as it is just a horizontal line through $y=-6$y=−6, shown in green. We can see that these two lines intersect at the point $\left(-5,-6\right)$(−5,−6). In other words, the lines intersect where $x=-5$x=−5 and $y=-6$y=−6, which is consistent with the $x=-5$x=−5 we got when solving algebraically.

In general, if we have a linear equation like $ax+b=cx+d$ax+b=cx+d, then we can check the solution by graphing $y=ax+b$y=ax+b and $y=cx+d$y=cx+d and finding the x-coordinate of the point of intersection.
There will usually be one solution, but sometimes we can see none or an infinite number.
Practice questions
Question 1
Consider the equation $\frac{3x}{5}-1=2$3x5−1=2.
Solve for the value of $x$x that satisfies the equation.
To verify the solution graphically, which two straight lines would need to be graphed?
$y=\frac{3x}{5}$y=3x5
A$y=\frac{3x}{5}+1$y=3x5+1
B$y=2$y=2
C$y=\frac{3x}{5}-1$y=3x5−1
DGraph the lines $y=\frac{3x}{5}-1$y=3x5−1 and $y=2$y=2 on the same plane.
Loading Graph...Hence find the value of $x$x that satisfies the two equations $y=\frac{3x}{5}-1$y=3x5−1 and $y=2$y=2 simultaneously.
Question 2
Consider the equation $2\left(x-1\right)-3=7$2(x−1)−3=7.
Solve for the value of $x$x that satisfies the equation.
To verify the solution graphically, which two straight lines would need to be graphed?
$y=2\left(x-1\right)+3$y=2(x−1)+3
A$y=7$y=7
B$y=2\left(x-1\right)-3$y=2(x−1)−3
C$y=2\left(x-1\right)+4$y=2(x−1)+4
DGraph the lines $y=2\left(x-1\right)-3$y=2(x−1)−3 and $y=7$y=7 on the same plane.
Loading Graph...Hence find the value of $x$x that satisfies the two equations $y=2\left(x-1\right)-3$y=2(x−1)−3 and $y=7$y=7 simultaneously.
Question 3
Using the graphs of $y=2x-7$y=2x−7 and $y=-2x+1$y=−2x+1, find the solution(s) of the equation $2x-7=-2x+1$2x−7=−2x+1.
Solving linear inequalities graphically
Similar to linear equations, we can also make a connection between linear inequalities and graphs of lines.
The key difference is that instead of just looking for where they intersect, but over what range of $x$x-values one line is above or below the other.
Previously, we learned how to solve linear inequalities. Remember that a linear inequality in $x$x will not involve $x^2$x2, $x^3$x3, $\frac{1}{x}$1x, or anything else. It will only ever involve $x$x being multiplied or divided by constants, or having constants added or subtracted.
In other words, the left hand side and right hand side of a linear equality will both be lines!
Think about it. If we have the linear inequality $3x-5<-5x+11$3x−5<−5x+11, the left hand side is the line $y_1=3x-5$y1=3x−5 and the right hand side is the line $y_2=-5x+11$y2=−5x+11.
We could solve the inequality algebraically like this.
| $3x-5$3x−5 | $<$< | $-5x+11$−5x+11 | |
| $8x-5$8x−5 | $<$< | $11$11 | Add $5x$5x to both sides |
| $8x$8x | $<$< | $16$16 | Add $5$5 to both sides |
| $x$x | $<$< | $2$2 | Divide both sides by $8$8. |
Or, we could realize that to solve $3x-5<-5x+11$3x−5<−5x+11 we just need to find for what values of $x$x the line $y_1=3x-5$y1=3x−5 is less than $y_2=-5x+11$y2=−5x+11.
We can graph both lines like this.
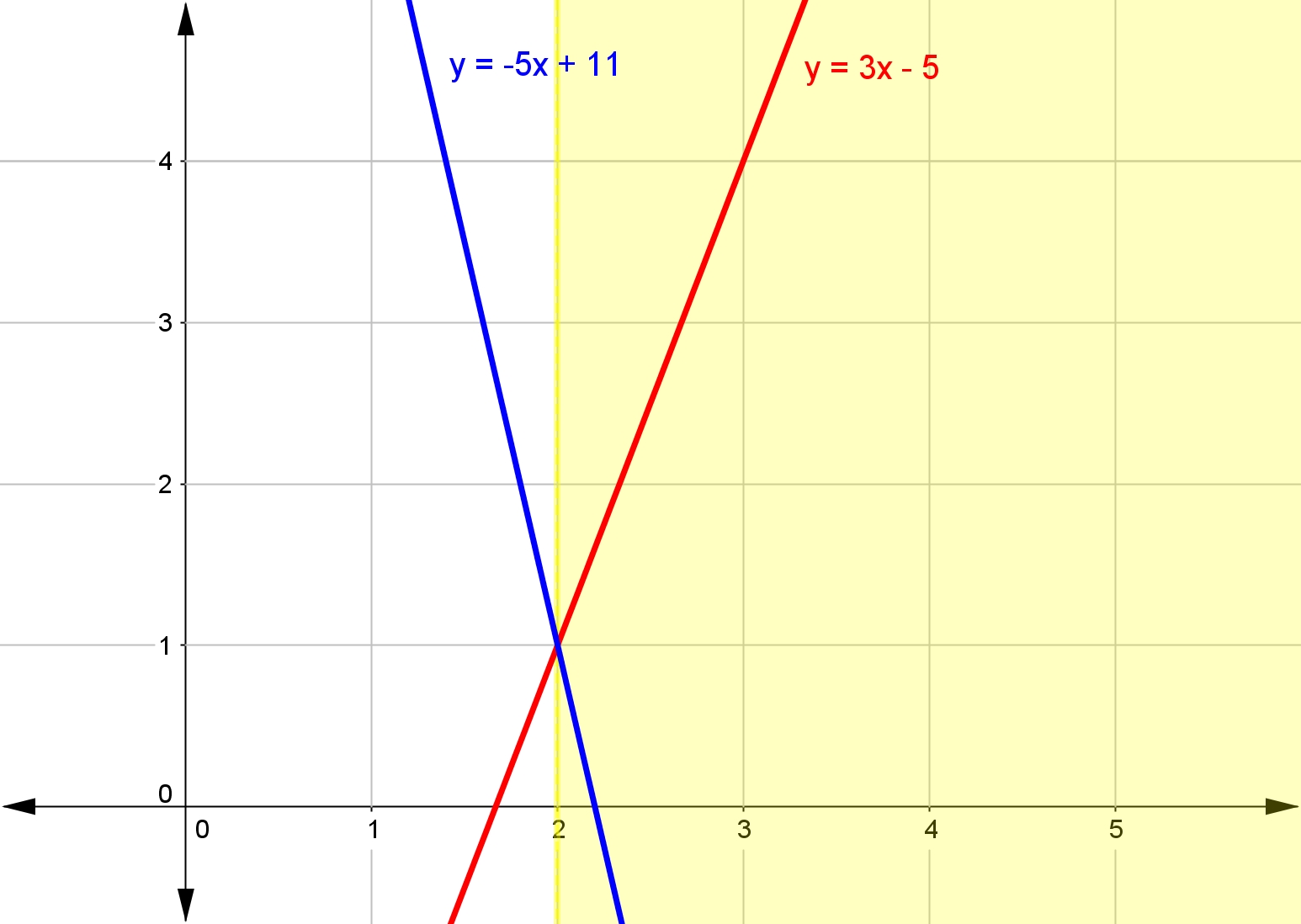
For what values of $x$x is the line $y_1=3x-5$y1=3x−5 less than $y_2=-5x+11$y2=−5x+11? In other words, when is the line $y_1=3x-5$y1=3x−5 below the line $y_2=-5x+11$y2=−5x+11?
Just as we found by solving the inequality algebraically, $y_1$y1 is below $y_2$y2 for $x<2$x<2.
Worked examples
Question 4
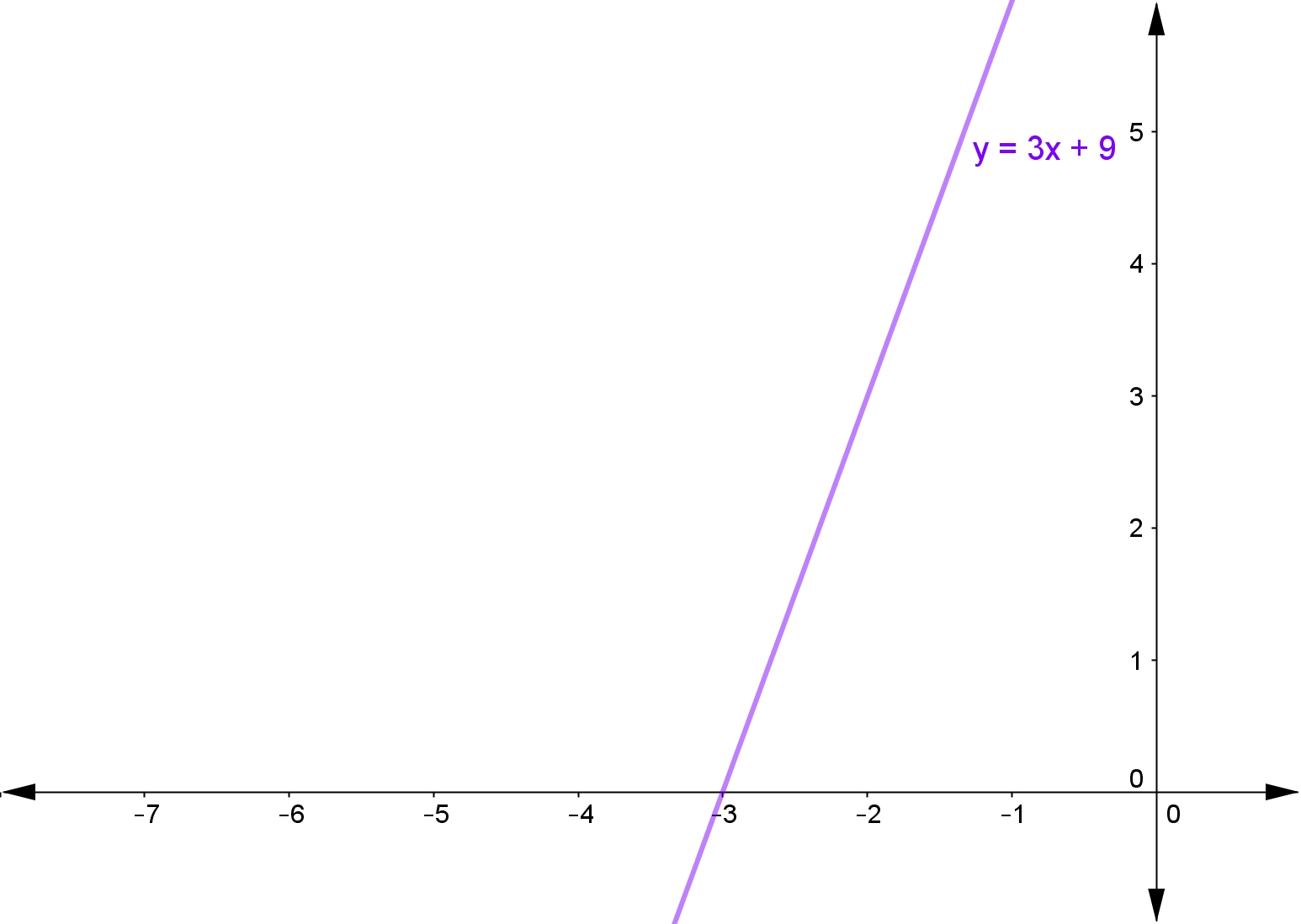
Using the above graph, state the solution to the linear inequality $3x+9\ge0$3x+9≥0 and plot the solution on a number line.
The solution to the inequality $3x+9\ge0$3x+9≥0 will be whenever the line $y=3x+9$y=3x+9 is above the line $y=0$y=0 (the $x$x-axis), in other words, when the line is positive.
We can see that this happens when $x\ge-3$x≥−3, which we can plot on the number line like this.

Question 5

Using the above graph, state the solution to the linear inequality $3x-21<9$3x−21<9 and plot the solution on a number line.
The solution to the inequality $3x-21<9$3x−21<9 will be whenever the line $y=3x-21$y=3x−21 is below the line $y=9$y=9.
We can see that this happens when $x<10$x<10, which we can plot on the number line like this.

Practice questions
Question 6
Consider the graph of $y=x-6$y=x−6.
Using the graph, state the solution of the inequality $x-6<0$x−6<0.
Question 7
Consider the graphs of $y=x+6$y=x+6 and $y=x-7$y=x−7.
Which of the following statements is true?
The inequality $x+6\ge x-7$x+6≥x−7 has one solution.
AThe inequality $x+6\ge x-7$x+6≥x−7 has an infinite number of solutions.
BThe inequality $x+6\ge x-7$x+6≥x−7 has no solutions.
C
Question 8
To solve the inequality $x\le\frac{x-3}{4}-1$x≤x−34−1, Tracy graphed $y=x-3$y=x−3. What other line would she need to graph to be able to solve the inequality graphically?
$y=4x+1$y=4x+1
A$y=\frac{x-3}{4}-1$y=x−34−1
B$y=x$y=x
C$y=4x+4$y=4x+4
D