8.03 Interpreting venn diagrams and two-way tables
Venn Diagrams
A Venn diagram is a way to display different groups of data. The idea of a Venn diagram was first introduced by John Venn in the late 1800's and they are still one of the most powerful ways to visualize relationships.
Let's say someone has the following clothes in their wardrobe.

Let's look at two different groups from these clothes, shirts and blue clothes.
| Shirts | Blue Clothes |
|---|---|
 |
 |
We now can display this in a Venn diagram, which is made from overlapping circles.

So we begin sorting the clothes, which is fairly straightforward.

The blue shirt corresponds to both sets, so it is put into the overlapping section in the center of the diagram.

We can use Venn diagrams in the same way to organize various types of data.
Worked example
Question 1
Using the numbers between $2$2and $20$20. Create two groups, one for even numbers and one for multiplies of $3$3.
Think: Let one circle represent even numbers and let the other circle represent multiples of $3$3. Where will numbers that are both even and a multiple of $3$3 fall?
Do: Numbers that are both even and a multiple of $3$3 will go in the overlapping portion in the center of the diagram.

To simplify things we can call the set of even numbers $E$E and the set of numbers that are multiples of $3$3 $M$M.
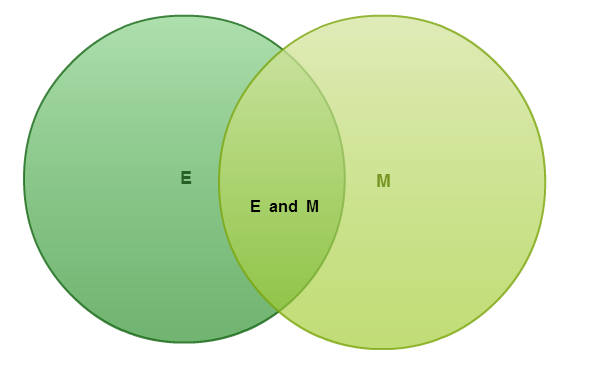
Now, we will look at each number from $2$2 and $20$20 and ask two questions. Is the number even? Is the number a multiple of $3$3?
If the number is only even in goes in the left circle, if it is only a multiple of $3$3 it goes in the right circle, if it is both even and a multiple of $3$3 it goes in the center, and if it is neither even nor a multiple of $3$3 it goes outside the circles as seen below.

Practice question
Question 2
Two-way frequency tables
Like Venn diagrams, two-way frequency tables are a visual way of representing information.
Two-way tables allow us to display and examine the relationship between two sets of categorical data. The categories are labeled at the top and the left side of the table, and the frequency of the different characteristics appear in the interior of the table. Often the totals of each row and column also appear.
The following two-way table was made by surveying $100$100 students who were $9$9th and $10$10th graders. They were asked two questions, if they are right or left-handed and if they were in the $9$9th or $10$10th grade, the results are as follows:
| Right-handed | Left-handed | Total | |
|---|---|---|---|
| 9th Grade | 43 | 9 | 52 |
| 10th Grade | 44 | 4 | 48 |
| Total: | 87 | 13 | 100 |
It's called a two-way table because we can read information from it in two directions. Here we have information about the two categories grade and handedness. If read across each row, we can tell how many students in each grade surveyed are right or left-handed. If we read down each column, we can tell how many of the right or left-handed people surveyed were in $9$9th grade and how many were in $10$10th grade.
Notice the last column contains the totals for each row and the last row contains the totals for each column. They both add up to $100$100 which is the total number of students surveyed. These are all called marginal frequencies. Think about how they are located on the edge of the table similar to the margins of a page.
Where a particular row and column overlap shows are how many people satisfy both categories. For example, there were $4$4 left-handed $10$10th graders surveyed. These are called joint frequencies because they represent where two categories join together.
Knowing there are $4$4 left-handed $10$10th graders we can find the proportion of $10$10th graders that are left-handed by dividing $4$4 by the total number of $10$10th graders $48$48. We get $\frac{4}{48}=\frac{1}{12}$448=112. So we can conclude that $\frac{1}{12}$112 or about $0.083$0.083 of the $10$10th graders surveyed were left-handed. This is called a conditional frequency because it represents what proportion of a group satisfies a given condition or qualification.
Worked example
Question 3
The following are the statistics of the passengers and crew who sailed on the Titanic on its fateful maiden voyage in $1912$1912.
| First Class | Second Class | Third Class | Crew | Total | |
|---|---|---|---|---|---|
| Survived | $202$202 | $118$118 | $178$178 | $212$212 | $710$710 |
| Died | $123$123 | $167$167 | $\editable{}$ | $696$696 | $1514$1514 |
| Total: | $325$325 | $285$285 | $\editable{}$ | $908$908 | $\editable{}$ |
a) According to the table, what is the total number of passengers (first, second, and third class) and crew on-board the ship?
Think: Adding the totals in the final column will give the total number of people on-board the ship.
Do:
| Total passengers and crew | $=$= | $710+1514$710+1514 |
| $=$= | $2224$2224 |
b) Find the missing values in the "Third Class" column.
Think: We now know the total number of passengers and crew. This number will also be the sum of the values in the "Total" row. We can use this to find the missing value of the total number of third class passengers. Once we have this we can use it to find the number of third class passengers who died.
Do:
| Total third class passengers | $=$= | $2224-908-285-325$2224−908−285−325 |
| $=$= | $706$706 |
| Third class passengers who died | $=$= | $\text{Total}-\text{survivors}$Total−survivors |
| $=$= | $706-178$706−178 | |
| $=$= | $528$528 |
c) What proportion of first class passengers survived?
Think: We need the fraction of first class survivors out of total number of first class passengers written as a decimal.
Do:
| Proportion of first class passengers that survived | $=$= | $\frac{\text{first class survivors}}{\text{total number first class passengers}}$first class survivorstotal number first class passengers |
| $=$= | $\frac{202}{325}$202325 | |
| $\approx$≈ | $0.62$0.62 |
d) What percentage of total passengers and crew survived?
Think: We need the fraction of total survivors out of total number of passengers and crew written as a percentage.
Do:
| Percentage of passengers and crew that survived | $=$= | $\frac{\text{total survivors}}{\text{total number passengers and crew}}$total survivorstotal number passengers and crew |
| $=$= | $\frac{710}{2224}\times100%$7102224×100% | |
| $\approx$≈ | $31.9%$31.9% |
Practice questions
QUESTION 4
The following table has been drawn up to show the results of a survey on smoking.
| Smokers | Non-smokers | |
|---|---|---|
| Men | $35$35 | $79$79 |
| Women | $56$56 | $139$139 |
How many of the people surveyed were smokers?
What percentage of women were non-smokers?
Write your answer as a percentage, correct to two decimal places.
What percentage of non-smokers were women? Write your answer correct to two decimal places.
QUESTION 5
Yuri surveyed a group of people about the type of jobs they had. He recorded the data in the following graph.
Complete the two way table with the information.
No Job Casual Part time Full time Men $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Women $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$
Question 6
$150$150 tennis players were asked whether they would support equal prize money for the women’s and men’s draw.
Support Do not support Males $\editable{}$ $35$35 Females $66$66 $12$12 Find the missing value in the table.
How many more players are there in support of equal prize money than those against it?
What percentage of the male tennis players support equal prize money?
Give your answer as a percentage to one decimal place if necessary.
QUESTION 7
Consider the Venn diagram:

Complete the table of values.
Play Rugby League Don't play Rugby League Play Rugby Union $\editable{}$ $\editable{}$ Don't play Rugby Union $\editable{}$ $\editable{}$
