12.04 Parabolas
Definition of a parabola
A parabola is one of the special shapes you can make when you slice a cone on an angle and is known as one of the conic sections.
The most basic parabolas are of the form $y=x^2$y=x2 and $x=y^2$x=y2. We have looked at parabolas of the form $y=x^2$y=x2 previously and the square root function which is half of the parabola of the form $x=y^2$x=y2.
A parabola is an arch-shaped curve such that any point on the curve is equal distance from a fixed point (called the focus) and a fixed line (called the directrix).
So all the points that are both equidistant from the focus and directrix can be joined together to form a parabola. We call all these points the locus of points.
Focus and directrix
Let's take a look at the graph of the parabola below, which includes the location of the focus and directrix.

Now, if we've placed the focus and directrix in the right location, distance A and distance B should be equal (because remember that the distance from any point on the curve to both the focus and directrix will be the same).
It's easy to see that distance $A$A = $5$5 units
To calculate distance $B$B we will use Pythagorean Theorem
| distance $B$B | $=$= | $\sqrt{4^2+3^2}$√42+32 |
| $=$= | $\sqrt{25}$√25 | |
| $=$= | $5$5 | |
And so we can see that both distances are the same!
Practice question
question 1
Consider the parabola $x^2=16y$x2=16y.
What are the coordinates of its vertex?
What is the equation of its axis of symmetry?
Solve for $a$a, the focal length of the parabola.
What are the coordinates of its focus?
What is the equation of its directrix?
Graphs of parabolas
As with any type of graph, it is helpful to have a standard form. We have four possible orientations for a parabola, opening up, opening down, opening right and opening left. Each of these can be identified from the standard form.
For an real number $a$a, with $a>0$a>0,
| Opening up: | $\left(x-h\right)^2=4a(y-k)$(x−h)2=4a(y−k) |
| Opening down: | $\left(x-h\right)^2=-4a(y-k)$(x−h)2=−4a(y−k) |
| Opening right: | $\left(y-k\right)^2=4a(x-h)$(y−k)2=4a(x−h) |
| Opening left: | $\left(y-k\right)^2=-4a(x-h)$(y−k)2=−4a(x−h) |
Key features of $\left(x-h\right)^2=\pm4a\left(y-k\right)$(x−h)2=±4a(y−k)
- $\left(h,k\right)$(h,k) is the vertex
- $\left(h,k+a\right)$(h,k+a) is the focus if opening up and $\left(h,k-a\right)$(h,k−a) is the focus if opening down
- $x=h$x=h is the axis of symmetry
- $y=k-a$y=k−a is the directrix if opening up and $y=k+a$y=k+a is the directrix if opening down
- $a$a is the focal length
Key features of $\left(y-k\right)^2=\pm4a\left(x-h\right)$(y−k)2=±4a(x−h)
- $\left(h,k\right)$(h,k) is the vertex
- $\left(h+a,k\right)$(h+a,k) is the focus if opening right and $\left(h-a,k\right)$(h−a,k) is the focus if opening left
- $y=k$y=k is the axis of symmetry
- $x=h-a$x=h−a is the directrix if opening right and $x=h+a$x=h+a is the directrix if opening left
- $a$a is the focal length
See some examples below of each of the four directions of opening.
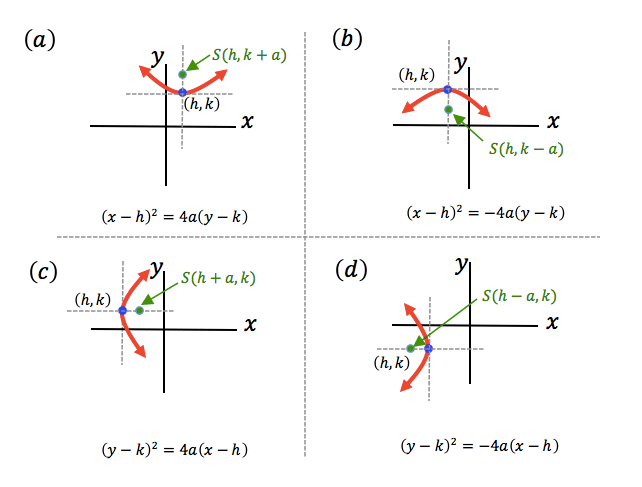
So if we wanted to construct an equation of a parabola that had its vertex at $\left(-3,4\right)$(−3,4), and its arms opening to the left, we could use an equation of the form$\left(y-4\right)^2=-4a\left(x+3\right)$(y−4)2=−4a(x+3).
Rearranging equations
When a parabola is given in one of the forms above, we can very quickly identify some of the key features and graph it. While we have looked at other techniques for graphing quadratic functions, let's look at how to rearrange parabolas to the forms above.
Worked examples
Question 2
Rearrange $y=x^2+6x+16$y=x2+6x+16. to one of the forms above and identify the vertex and direction of opening.
Think: Since the $x$x term is squared, we want to rearrange to the form $\left(x-h\right)^2=4a\left(y-k\right)$(x−h)2=4a(y−k), this will involve completing the square.
Do:
| $y$y | $=$= | $x^2+6x+16$x2+6x+16 |
Given |
| $x^2+6x+16$x2+6x+16 | $=$= | $y$y |
Swap sides |
| $x^2+6x+9-9+16$x2+6x+9−9+16 | $=$= | $y$y |
Complete the square for $x^2+6x$x2+6x |
| $\left(x+3\right)^2+7$(x+3)2+7 | $=$= | $y$y |
Combine Like Terms |
| $\left(x+3\right)^2$(x+3)2 | $=$= | $y-7$y−7 |
Subtract $7$7 from both sides |
The parabola in vertex form is shown as type (a) above, with a vertex of $\left(-3,7\right)$(−3,7) and opening upwards.
Question 3
Identify the focal length and the focus of the parabola $2\left(x-3\right)^2=y+5$2(x−3)2=y+5.
Think: Let's start be getting it to the desired form $\left(x-3\right)^2=\frac{1}{2}\left(y-5\right)$(x−3)2=12(y−5) or $\left(x-3\right)^2=4\left(\frac{1}{8}\right)\left(y-5\right)$(x−3)2=4(18)(y−5).
Do: The focal length $a=\frac{1}{8}$a=18 and the coordinates of the focus are $\left(3\frac{1}{8},-5\right)$(318,−5).
Question 4
Rearrange the quadratic $y=2x^2-20x+32$y=2x2−20x+32 to the appropriate general form of a quadratic, then graph.
Think: From what we have seen in previous courses, we know immediately that the parabola opens upward, so it is of the form $\left(x-h\right)^2=4a\left(y-k\right)$(x−h)2=4a(y−k), where $p>0$p>0.
Do: We can rearrange the original equation, by completing the square, to vertex form as follows:
| $y$y | $=$= | $2x^2-20x+32$2x2−20x+32 |
| $y$y | $=$= | $2\left(x^2-10x+16\right)$2(x2−10x+16) |
| $y$y | $=$= | $2\left(x^2-10x+25-9\right)$2(x2−10x+25−9) |
| $y$y | $=$= | $2\left[\left(x-5\right)^2-9\right]$2[(x−5)2−9] |
| $y$y | $=$= | $2\left(x-5\right)^2-18$2(x−5)2−18 |
| $\left(x-5\right)^2$(x−5)2 | $=$= | $\frac{1}{2}\left(y+18\right)$12(y+18) |
| $\left(x-5\right)^2$(x−5)2 | $=$= | $4\times\left(\frac{1}{8}\right)\left(y+18\right)$4×(18)(y+18) |
From this form we can easily read off the following features:
- Vertex has coordinates $\left(5,-18\right)$(5,−18)
- Focal length is $a=\frac{1}{8}$a=18
- The focus is located at $\left(5,-18+\frac{1}{8}\right)=\left(5,-17\frac{7}{8}\right)$(5,−18+18)=(5,−1778)
- The directrix is the line $x=-18-\frac{1}{8}=-18\frac{1}{8}$x=−18−18=−1818
Here is the graph:

Practice questions
Question 5
Consider the parabola represented by the equation $y-4=\left(x+5\right)^2$y−4=(x+5)2.
What are the coordinates of the vertex?
Give your answer in the form $\left(a,b\right)$(a,b).
In which direction does this parabola open?
To the right
ADownwards
BUpwards
CTo the left
D
Question 6
Consider the parabola represented by the equation $x-4=\left(y+2\right)^2$x−4=(y+2)2.
What are the coordinates of the vertex?
Give your answer in the form $\left(a,b\right)$(a,b).
In which direction does this parabola open?
Upwards
ATo the left
BDownwards
CTo the right
D
Finding equations of parabolas
Given certain identifying information, it is possible to construct the equation of a parabola. As we have seen above, there are four basic orientations to consider as shown in the diagram below. In each of the parabolas, the focus $S$S is positioned on the axis of symmetry of the parabola and on the same side that the parabola is opening to.
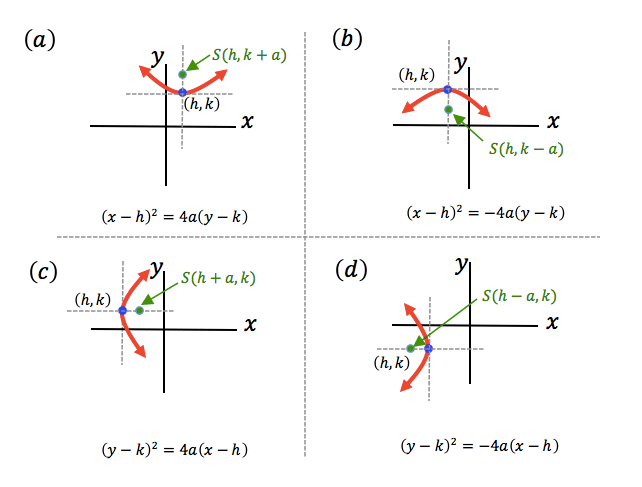
Consider the following examples where we can use this diagram to construct the equation.
Worked examples
Question 7
A parabola has its vertex at the origin. It's focus lies on the y-axis, $5$5 units directly below the vertex. What is the equation of this parabola?
Think: Diagram (b) above shows a focus directly below the vertex. We are looking for an equation of the form $\left(x-h\right)^2=4a(y-k)$(x−h)2=4a(y−k).
Do: Since the vertex is at the origin, we have that $\left(h,k\right)=\left(0,0\right)$(h,k)=(0,0), we see that the basic form of the equation becomes $x^2=-4ay$x2=−4ay. We also know that the focal length $a=5$a=5, and because the vertex is at the origin, it must mean that the coordinates of the focus are $\left(0,-5\right)$(0,−5).
The equation becomes $x^2=-20y$x2=−20y., and the directrix is the line $y=-5$y=−5.
Question 8
Find the equation of a parabola with its vertex at $\left(-4,3\right)$(−4,3) and its directrix at $x=-9$x=−9.
Think: If we know the directrix and the vertex, we can work backwards to find the focal length.
Do: Since the directrix is the line $x=-9$x=−9 and the vertex is at $\left(-4,3\right)$(−4,3), then the focal length must be $5$5 (in other words the gap between $x=-9$x=−9 and $x=-4$x=−4 is clearly $5$5).
The directrix is on the opposite side of the curve to the focus, so the focus must have the coordinates $\left(1,3\right)$(1,3).
Clearly the curve opens outward to the right, and this means (referring to the diagram) that the equation has the form $\left(y-k\right)^2=4a\left(x-h\right)$(y−k)2=4a(x−h).
The equation is therefore $\left(y-3\right)^2=20\left(x+4\right)$(y−3)2=20(x+4).
Question 9
A certain parabola has a horizontal axis of symmetry, a vertex at $\left(2,6\right)$(2,6) and passes through the point $\left(-30,-10\right)$(−30,−10). Find the equation of the parabola.
Think: If the parabola passes through the point $\left(-30,-10\right)$(−30,−10), and the vertex is at $\left(2,6\right)$(2,6), then quite clearly, the parabola is opening up to the left. So the correct form to choose is form (d) above given by $\left(y-k\right)^2=-4a\left(x-h\right)$(y−k)2=−4a(x−h).
Do: Therefore the equation becomes $\left(y-6\right)^2=-4a\left(x-2\right)$(y−6)2=−4a(x−2). Again, the point $\left(-30,-10\right)$(−30,−10) satisfies the equation, so we need to solve $\left(-10-6\right)^2=-4a\left(-30-2\right)$(−10−6)2=−4a(−30−2) for $a$a.
Thus:
| $\left(-16\right)^2$(−16)2 | $=$= | $-4a\left(-32\right)$−4a(−32) |
| $\left(-16\right)^2$(−16)2 | $=$= | $128a$128a |
| $256$256 | $=$= | $128a$128a |
| $\therefore$∴ $a$a | $=$= | $2$2 |
The equation of the parabola is therefore $\left(y-6\right)^2=-8\left(x-2\right)$(y−6)2=−8(x−2). Its directrix is the vertical line $x=4$x=4 and the focus has the coordinates $\left(0,6\right)$(0,6).
Practice questions
Question 10
A particular parabola with a vertex at the origin opens left and passes through the point $\left(-1,-6\right)$(−1,−6). By determining the focal length $a$a or otherwise, find the equation of the parabola.
Question 11
A certain parabola has a horizontal axis of symmetry, a vertex at $\left(-1,-2\right)$(−1,−2) and passes through the point $\left(-3,-10\right)$(−3,−10). By determining the focal length $a$a, find the equation of the parabola.
Question 12
A parabola has its vertex at the origin. It has a focal length measuring $a=4$a=4 units, and its focus lies on the $x$x-axis.
State both possible equations of the parabola.
Solve applications involving parabolic functions
Parabolas have many applications. Below are a few examples.
It is the path taken by a cannon ball when fired out of a cannon at some particular angle of elevation. It is the path of a stream of water as it pushes out of a hose fitting. In fact the parabolic trajectory is a universal one - a stone thrown by someone on the surface of the moon follows a parabola.
It is the natural shape formed by the cable on the Brooklyn Bridge and the Golden Gate Bridge in San Francisco.
The reflective property
The reflective property is perhaps the most scientifically utilized feature of the parabola. Radio telescopes and lighthouses work because of it. Torches and car headlights use parabolic mirrored surfaces that reflect light rays in such a way as to prevent the light from scattering too much. Concrete constructions of parabolic surfaces were even used in England in World War 2 to bring the reflection of distant sounds of enemy aircraft to a single point, so they could be heard.
Light rays emanating from the focus of a parabola will strike the inside surface (assuming its made of a mirrored compound) and be reflected back along lines parallel to the parabola's axis of symmetry.
The reflection property is illustrated in the following diagram.

The light ray shown in blue highlights the Law of reflection. The law guarantees that the two angles $SPN$SPN and $NPQ$NPQ measured against the normal $PN$PN as the incident angle $i^{\circ}$i∘ and the reflection angle $r^{\circ}$r∘ are equal irrespective of where the ray strikes.
Worked example
Question 13
A $70$70 meter antenna operates at the Tidbinbilla tracking station. It is the largest steerable parabolic antenna in the Southern Hemisphere. Weighing more than $3000$3000 metric tons it rotates on a film of oil. The reflector surface is made up of $1272$1272 aluminum panels with a total surface area of $4180$4180 square meters. What is the depth of the dish at the center?

Image source: CSIRO
Think: Assuming that the focal length of the parabola is $27$27 meters and the diameter of the dish is $70$70 meters, we seek an equation for the parabola relative to the coordinate axes and the depth of the dish at the center.
Do: The form of the equation is given as $x^2=4ay$x2=4ay, opening from above with the vertex at the origin. Since the focal length is $27$27, the equation becomes $x^2=108y$x2=108y.
Because the diameter is $70$70 meters, the point $B$B in the photograph must have coordinates given by $\left(35,y_B\right)$(35,yB) where the value of $y_B$yB can be found.
| $x^2$x2 | $=$= | $108y$108y |
| $35^2$352 | $=$= | $108\left(y_B\right)$108(yB) |
| $1225$1225 | $=$= | $108\left(y_B\right)$108(yB) |
| $\therefore$∴ $y_B$yB | $\approx$≈ | $11.343$11.343 |
This means the depth of the dish at the center is $11.343$11.343 meters.
Practice questions
Question 14
A satellite dish is parabolic in shape, with a diameter of $8$8 meters. Incoming signals are reflected to one collection point, the focus of the parabola, marked as point $F$F on the diagram (not to scale). The focus is positioned such that the focal length is $4$4 meters.

Using $\left(0,0\right)$(0,0) as the vertex of the parabola, solve for $d$d, the depth of the dish in meters.
Question 15
A parabolic antenna has a cross-section of width $16$16 m and depth of $2$2 m. All incoming signals reflect off the surface of the antenna and pass through the focus at $F$F. Note: Image is not to scale

Placing the vertex of the antenna at $\left(0,0\right)$(0,0), we can model the surface of the antenna by the parabola with equation $y^2=4ax$y2=4ax.
State the equation of parabola.
For best reception, at what coordinate should the receiver be placed?
Question 16
When a fire hose is turned on, the height $h$h meters of the stream of water is described by $h=-0.25d\left(d-32\right)$h=−0.25d(d−32), where $d$d meters is the horizontal distance from the hose.
Let the hose be positioned at $\left(0,0\right)$(0,0). Use the graph to determine how far from the hose the water reaches its maximum height above ground.
$\editable{}$ meters from the hose
Using the graph, determine the maximum height reached by the hose.
There are two points on the path where the water is at a height of $48$48 meters above the ground. What is the horizontal distance between these two points?
Determine the height of the water above the ground when it is a horizontal distance of $6$6 meters from where the fire is.
For what values of $d$d is the model valid?
$d\le32$d≤32 and $d\ge0$d≥0
A$d<0$d<0 and $d<32$d<32
B$d\ge0$d≥0 and $d>32$d>32
C$d>32$d>32 and $d<0$d<0
D
