12.03 Manipulating circle equations
Explore the definition of circles in the coordinate plane
When we looks at graphs of functions or relations, we concentrate our focus on key characteristics of a graph. For example, when we look at a parabola of a quadratic function, we might focus on the turning point or the $x$x intercepts. Now we're interested in examining the graph of a circle, and to do that we need to concentrate our focus on two key characteristics.
A circle can be uniquely defined by the center and the radius
The center is the point which every point $\left(h,k\right)$(h,k) on the circle is equidistant from
The radius is the distance from the center to any point on the circle
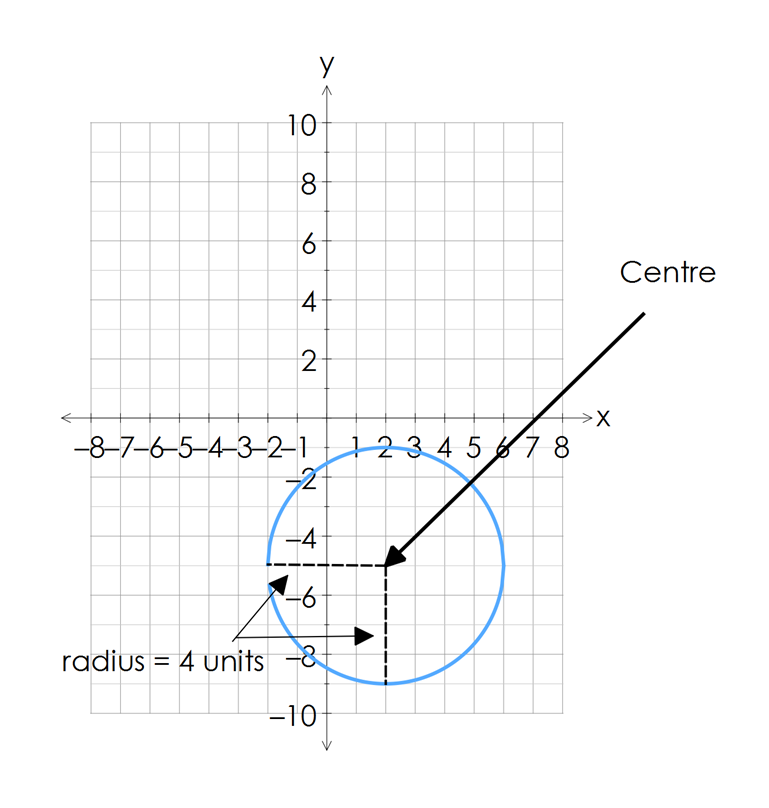
On the graph below, you can see, by inspection, that the center of the circle is $(2,-5)$(2,−5)
We can determine the radius of the circle by counting the number of units from the center, out to the left or right of the center, or directly up or down from the center. So for this graph the radius is $4$4 units.
Practice questions
QUESTION 1
Consider the circle in the graph.
State the coordinates of the center in the form $\left(a,b\right)$(a,b).
State the radius.
QUESTION 2
Consider the graph of the circle shown below.
Complete the statement.
Every point on the circle is exactly $\editable{}$ units away from the point
$\left(\editable{},\editable{}\right)$(,)
Graph and state equations of circles at the origin
We have looked at how to graph different kinds of equations such as straight lines and parabolas. We have seen how to graph and determine the equation of circles previously. Below is a quick refresher.
The following interactive allows you to explore the standard form equation of a circle. It shows how the equation changes as the radius $r$r changes. To change the radius, just drag the $r$r slider.
$x^2+y^2=r^2$x2+y2=r2
where $\left(x,y\right)$(x,y) is the center of the circle and $r$r is the radius
Proof:
This formula is derived using Pythagoras' theorem. Consider the following graph, which is a circle with the center at $\left(0,0\right)$(0,0) and a radius of $5$5 units. The blue radius touches the circle at $\left(4,3\right)$(4,3).
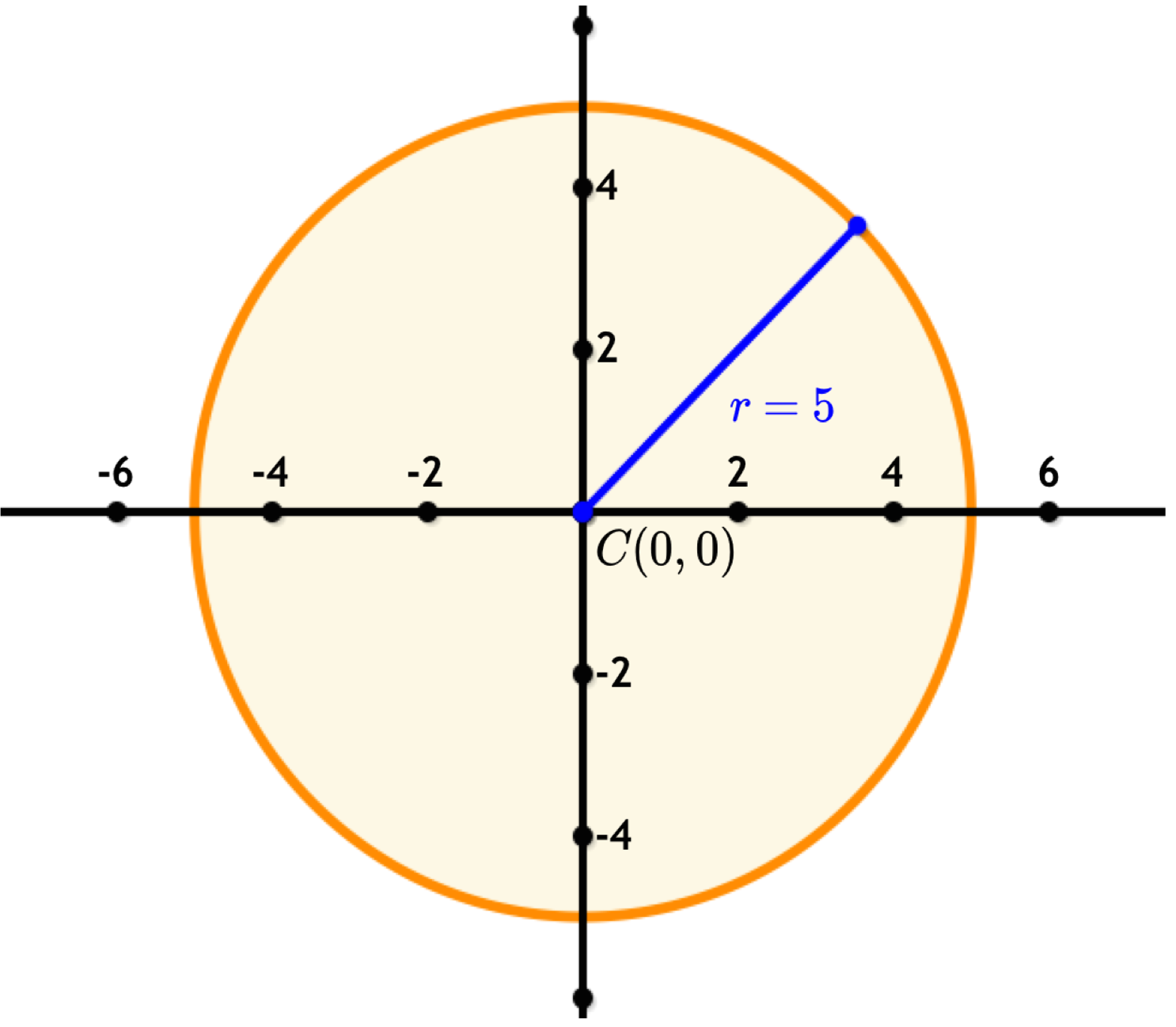
Let's draw in a right triangle:

Using Pythagoras' theorem:
| $3^2+4^2$32+42 | $=$= | $9+16$9+16 |
| $=$= | $25$25 | |
| $=$= | $r^2$r2 |
$\therefore$∴ $x^2+y^2=r^2$x2+y2=r2
Practice questions
Question 3
State the equation of the circle.
Question 4
A circle has its center at the origin and a radius of $4$4 units.
Draw a graph of this circle.
Loading Graph...Write the equation of the circle.
Graph and state equations of circles with any center
Now that we know $x^2+y^2=r^2$x2+y2=r2 represents a circle with center at the origin, $\left(0,0\right)$(0,0), and radius, $r$r, we can explore circles not centered at the origin. The following interactive allows you to explore the standard form equation of a circle. It shows how the equation changes as the coordinates of the center $\left(h,k\right)$(h,k) and the radius $r$r change. To move the circle, drag the sliders for $h$h and $k$k, the center coordinates of the circle, while to change the radius, just drag the $r$r slider.
$\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2
where $\left(h,k\right)$(h,k) is the coordinates of the center of the circle
and $r$r is the radius of the circle
Practice questions
Question 5
The equation of a circle is given by $\left(x+4\right)^2+\left(y-2\right)^2=25$(x+4)2+(y−2)2=25.
Find the coordinates of the center of this circle.
What is the radius of the circle?
Plot the graph for the given circle.
Loading Graph...
Question 6
A circle has its center at ($3$3,$3$3) and a radius of 6 units.
Plot the graph for the given circle.
Loading Graph...Write the equation of the circle.
Domain and range of circles
The diagram below shows that the domain of a circle consists of all $x$x-values within the interval $a-r\le x\le a+r$a−r≤x≤a+r and the range of of a circle consists of all $y$y-values within the interval $b-r\le y\le b+r$b−r≤y≤b+r.

We can also write the domain in interval notation as $\left[a-r,a+r\right]$[a−r,a+r], and the range in interval notation as $\left[b-r,b+r\right]$[b−r,b+r].
Notice that while a circle is a relation, it is not a function as it would fail the vertical line test.
Practice questions
Question 7
Consider the graph of the circle shown below.
State the domain of the graph in interval notation.
State the range of the graph in interval notation.
Question 8
Consider the equation $\left(x+5\right)^2+\left(y+3\right)^2=16$(x+5)2+(y+3)2=16.
Plot the graph described by the equation.
Loading Graph...State the domain of the graph, using interval notation.
State the range of the graph, using interval notation.
Question 9
A circle has a domain of $\left[2,10\right]$[2,10] and a range of $\left[-4,4\right]$[−4,4].
Plot the circle.
Loading Graph...State the equation for the circle in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2.
Completing the square in circles
Typically we are given the equation of a circle in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2. Ideally, we would like to express any equation of a circle in this form since we can immediately identify its center and radius:
- $\left(h,k\right)$(h,k) is the center of the circle.
- $r$r is the radius of the circle.
But generally speaking, the equation of a circle can be expressed in many ways. For instance, the following three equations all represent the same circle.
- $\frac{\left(x-2\right)^2}{25}+\frac{\left(y-3\right)^2}{25}=1$(x−2)225+(y−3)225=1
- $\left(x-2\right)^2+\left(y-3\right)^2=25$(x−2)2+(y−3)2=25
- $x^2+y^2-4x-6y=12$x2+y2−4x−6y=12
In order to express the above equations in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2, we can manipulate both sides by multiplying or by completing the square.
Worked examples
question 10
Consider the equation of the circle $x^2+y^2-4x-6y=12$x2+y2−4x−6y=12.
Rewrite the equation in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2.
Think: Completing the square allows us to rewrite the quadratic expressions in $x$x and $y$y to be perfect squares of the form $\left(x-h\right)^2$(x−h)2 and $\left(y-k\right)^2$(y−k)2.
We can first reorder the terms into a more convenient form:
$x^2-4x+y^2-6y=12$x2−4x+y2−6y=12
Then to complete the square in $x$x we look at the expression $x^2-4x$x2−4x, halve and square the coefficient of $x$x, and then add the result to both sides of the equation.
Do: Halving and squaring $-4$−4 gives a result of $4$4, so we add this result to both sides of the equation:
$x^2-4x+4+y^2-6y=12+4$x2−4x+4+y2−6y=12+4
Similarly, to complete the square in $y$y we add $9$9 to both sides of the equation:
$x^2-4x+4+y^2-6y+9=12+4+9$x2−4x+4+y2−6y+9=12+4+9
Putting this together, we get the following steps:
| $x^2+y^2-4x-6y$x2+y2−4x−6y | $=$= | $12$12 | (Writing down the equation) |
| $x^2-4x+y^2-6y$x2−4x+y2−6y | $=$= | $12$12 | (Swapping the order of terms) |
| $x^2-4x+4+y^2-6y+9$x2−4x+4+y2−6y+9 | $=$= | $12+4+9$12+4+9 | (Completing the square for $x$x and $y$y) |
| $x^2-4x+4+y^2-6y+9$x2−4x+4+y2−6y+9 | $=$= | $25$25 | (Simplifying the constant terms) |
| $\left(x-2\right)^2+\left(y-3\right)^2$(x−2)2+(y−3)2 | $=$= | $25$25 | (Factoring the perfect squares) |
The equation of the circle is then $\left(x-2\right)^2+\left(y-3\right)^2=25$(x−2)2+(y−3)2=25.
Reflect: The equation of the circle centered at $\left(2,3\right)$(2,3) with radius $5$5 can be expressed by the equation $\left(x-2\right)^2+\left(y-3\right)^2=25$(x−2)2+(y−3)2=25 or the equation $x^2+y^2-4x-6y=12$x2+y2−4x−6y=12.
Question 11
Consider the equation of the circle $2x^2+4x+2y^2+24y+2=0$2x2+4x+2y2+24y+2=0.
Rewrite the equation in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2 and then graph.
Think: Completing the square allows us to rewrite the terms containing $x$x and $y$y in the form $\left(x-h\right)^2$(x−h)2 and $\left(y-k\right)^2$(y−k)2. Before we do so, it will be more convenient for the coefficients of $x^2$x2 and $y^2$y2 to be $1$1.
Do: In this case, the coefficient of both $x^2$x2 and $y^2$y2 is $2$2, so we can divide both sides of the equation by $2$2:
$x^2+2x+y^2+12y+1=0$x2+2x+y2+12y+1=0
Then we can move the constant term by subtracting $1$1 from both sides:
$x^2+2x+y^2+12y=-1$x2+2x+y2+12y=−1
Now we can complete the square in $x$x and $y$y:
$x^2+2x+1+y^2+12y+36=-1+1+36$x2+2x+1+y2+12y+36=−1+1+36
Putting this together, we get the following steps:
| $2x^2+4x+2y^2+24y+2$2x2+4x+2y2+24y+2 | $=$= | $0$0 | (Writing down the equation) |
| $x^2+2x+y^2+12y+1$x2+2x+y2+12y+1 | $=$= | $0$0 | (Dividing both sides by $2$2) |
| $x^2+2x+y^2+12y$x2+2x+y2+12y | $=$= | $-1$−1 | (Moving the constant to one side) |
| $x^2+2x+1+y^2+12y+36$x2+2x+1+y2+12y+36 | $=$= | $-1+1+36$−1+1+36 | (Completing the square for $x$x and $y$y) |
| $x^2+2x+1+y^2+12y+36$x2+2x+1+y2+12y+36 | $=$= | $36$36 | (Simplifying the constant terms) |
| $\left(x+1\right)^2+\left(y+6\right)^2$(x+1)2+(y+6)2 | $=$= | $36$36 | (Factoring the perfect squares) |
So the equation of the circle can be expressed in the form $\left(x+1\right)^2+\left(y+6\right)^2=36$(x+1)2+(y+6)2=36.
Reflect: The center of the circle is $\left(h,k\right)=\left(-1,-6\right)$(h,k)=(−1,−6) and the radius is $r=6$r=6. From this, we can draw the equation of the circle as shown below.
 |
| Graph of the circle $2x^2+4x+2y^2+24y+2=0$2x2+4x+2y2+24y+2=0 |
Practice questions
question 12
The following equation describes a circle:
$x^2+y^2+2x+4y=11$x2+y2+2x+4y=11
By completing the squares, express the equation of the circle in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2.
Hence find the coordinates of the center of the circle.
Hence also, what is the radius of the circle?
Plot the graph for the given circle.
Loading Graph...
question 13
The following equation describes a circle:
$4x^2+4y^2+36x-12y+41=0$4x2+4y2+36x−12y+41=0
By completing the squares, express the equation of the circle in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2.
Hence find the coordinates of the center of the circle.
Hence also, what is the radius of the circle?
Plot the graph for the given circle.
Loading Graph...
question 14
Consider the equation of a circle given by $x^2-2x+y^2-16y-16=0$x2−2x+y2−16y−16=0.
Rewrite the equation of the circle in standard form.
What are the coordinates of the center of this circle?
What is the radius of this circle?
Graph this circle on the axes below:
Loading Graph...
Applications of circles
We can make use of our knowledge of circles and their equations to solve various problems involving circles. Let's take a look at a few properties.
- The equation of a circle describes all of the points that lie exactly a distance of $r$r away from the center point $\left(h,k\right)$(h,k). Any points which are closer than $r$r units to the center lie inside the circle, and any points that are further than $r$r units from the center lie outside the circle.

A circle, with points at different distances from the center.
- Two points which lie on opposite ends of a diameter of a circle have the center of the circle as their midpoint.

Two points at opposite ends of a diameter.
- The area of a circle of radius $r$r is given by $A=\pi r^2$A=πr2. Similarly, the length of the circumference of a circle of radius $r$r is given by $C=2\pi r$C=2πr.
- A circle can be inscribed in a square as in the image below. This square is the smallest possible square that can fit around the circle, which touches at four points and has side lengths equal to the length of the diameter of the circle.

A circle inscribed inside a square.
Let's go through an example now.
Worked example
question 15
A circle of radius $3$3 units is centered at the point $\left(12,5\right)$(12,5). What is the shortest distance from the origin to the circle?
Think: We can start by drawing a diagram of the situation, to easily see what's going on.

From the diagram, we can see that the closest point to the origin is between the center and the origin. In fact, if we draw a line from the origin to the center of the circle it will intersect the circle at the closest point.

This means that the shortest distance from the origin to the circle will be equal to the distance between the origin and the center, minus the radius of the circle.

Do: We know that the radius of the circle is $3$3 units, and we can use the distance formula to find the distance between the origin and the center:
| $d$d | $=$= | $\sqrt{\left(12-0\right)^2+\left(5-0\right)^2}$√(12−0)2+(5−0)2 |
| $=$= | $\sqrt{12^2+5^2}$√122+52 | |
| $=$= | $\sqrt{144+25}$√144+25 | |
| $=$= | $\sqrt{169}$√169 | |
| $=$= | $13$13 |
Subtracting the radius from this, we can see that the shortest distance from the origin to the circle is $13-3=10$13−3=10 units.
Practice questions
Question 16
The endpoints of the diameter of a circle are $\left(-5,-3\right)$(−5,−3) and $\left(-15,-15\right)$(−15,−15).
What are the coordinates of the center of the circle?
What is the exact radius of the circle?
Hence find the equation of the circle which has $\left(-5,-3\right)$(−5,−3) and $\left(-15,-15\right)$(−15,−15) as endpoints of its diameter.
Question 17
Naval ship $A$A picks up the signal of another vessel $45$45 km away. Ship $A$A can also see that there is a partner naval ship, ship $B$B, $30$30 km south and $40$40 km west of it.
Using $\left(0,0\right)$(0,0) as the position of naval ship $A$A, determine the distance between naval ships $A$A and $B$B.
Could the signal that was picked up be coming from naval ship $B$B?
No
AYes
B