11.04 The normal distribution
When we have a set of univariate data, it often happens that most of the measurements will be clustered close to the mean value with the density of the observations falling off with distance away from the mean. Results of this kind displayed in a histogram show a central peak with columns of decreasing height on each side of the mean.

A data set that is symmetrical and bell-shaped about the mean, and which meets certain more precise shape requirements, is said to have a normal distribution.
The shape of the normal distribution will depend on its mean ($\mu$μ) and standard deviation $(\sigma)$(σ). The mean is where the graph peaks
For the normal distribution, the mean is exactly in the middle, so $50%$50% of the values are above the mean and $50%$50% of the values are below the mean.
The lower the standard deviation, the more clustered the scores will be around the mean. Conversely, the higher the standard deviation, the more spread the scores will be.
For example, this distribution curve comes from a data set that has a very small standard deviation, $\sigma=0.2$σ=0.2, and hence is clustered tightly around the mean:

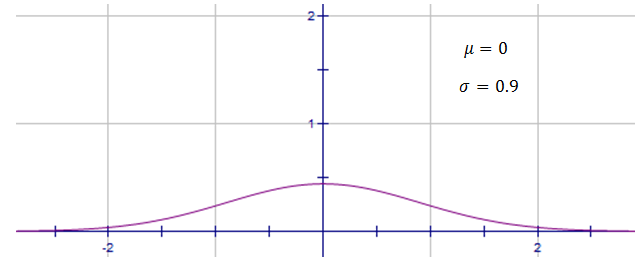
whereas this normal distribution has a larger standard deviation, $\sigma=0.9$σ=0.9, and hence is quite spread.
To see how a change in the mean and standard deviation affects the shape of the normal distribution curve, check out this graph. By moving the sliders around you can vary the mean and standard deviation, and see how the bell curve changes as a result.
Practice questions
QUESTION 1
Which of the following sets of data is approximately normally distributed?
- ABC
QUESTION 2
Which two of the following statements are true for a normal distribution curve?
There are the same number of scores above and below the mean.
AThe curve is symmetrical.
BThe fewest scores lie around the mean.
CThe curve is asymmetrical.
D
QUESTION 3
A sample of professional basketball players is normally distributed and gives the mean height as $199$199 cm with a standard deviation of $10$10 cm.
How tall is a basketball player who is $3$3 standard deviations above the mean?
How tall is a basketball player who is $1.5$1.5 standard deviations below the mean?