10.08 Quadratics in vertex form
Graph quadratics in vertex form
We have already learned how to complete the square to rewrite a quadratic in a different form. This form that we get from completing the square is called vertex form. It gets its name from the fact that we can easily see the vertex of the quadratic by simply looking at the equation. This makes it really easy to graph the quadratic.
The vertex form of a quadratic where $a\ne0$a≠0 and the vertex is $\left(h,k\right)$(h,k) is:
$y=a\left(x-h\right)^2+k$y=a(x−h)2+k
Graph using the vertex and y-intercept
The vertex is the turning point of the parabola and it lies on the axis of symmetry. From the equation $y=a\left(x-h\right)^2+k$y=a(x−h)2+k, we can see that the turning point has the coordinates $\left(h,k\right)$(h,k).
If we compare the quadratic parent function $y=x^2$y=x2, whose vertex is at $\left(0,0\right)$(0,0), to $y=a\left(x-h\right)^2+k$y=a(x−h)2+k, then we can think of the second equation and its graph as a transformation of $y=x^2$y=x2:
- $h$h represents the number of units that $y=x^2$y=x2 is translated horizontally, and
- $k$k represents the number of units that $y=x^2$y=x2 is translated vertically.
Note that with the direction of the horizontal translation:
-
If the equation is $y=\left(x+1\right)^2-3$y=(x+1)2−3, the horizontal translation is $1$1 unit to the left.
-
If the equation is $y=\left(x-1\right)^2-3$y=(x−1)2−3, the horizontal translation is $1$1 unit to the right.
Let's look at the quadratic $y=-2\left(x-3\right)^2-3$y=−2(x−3)2−3.
We can see that the quadratic has a vertex or turning point at $\left(3,-3\right)$(3,−3). Because the leading coefficient is negative we know that the parabola opens downward which makes the vertex a maximum.
With just these two pieces of information we can draw a rough sketch of the curve.
But many parabolas have a vertex at $\left(3,-3\right)$(3,−3) that is a maximum. To be able to graph the parabola more accurately with the correct amount of steepness, we need another piece of information. We need another point on the graph.
The $y$y-intercept is a good point to use because it is quick to find. We can find the $y$y-intercept by setting $x$x to $0$0.
| $y$y | $=$= | $-2\left(x-3\right)^2-3$−2(x−3)2−3 |
| $=$= | $-2\left(0-3\right)^2-3$−2(0−3)2−3 | |
| $=$= | $-2\times\left(-3\right)^2-3$−2×(−3)2−3 | |
| $=$= | $-2\times9-3$−2×9−3 | |
| $=$= | $-18-3$−18−3 | |
| $=$= | $-21$−21 |
$x$x-intercept occurs where the value of $y$y is $0$0
$y$y-intercept occurs where the value of $x$x is $0$0
Now we can sketch the curve. Graphing the vertex $\left(3,-3\right)$(3,−3) as a maximum and the $y$y-intercept of $-21$−21:
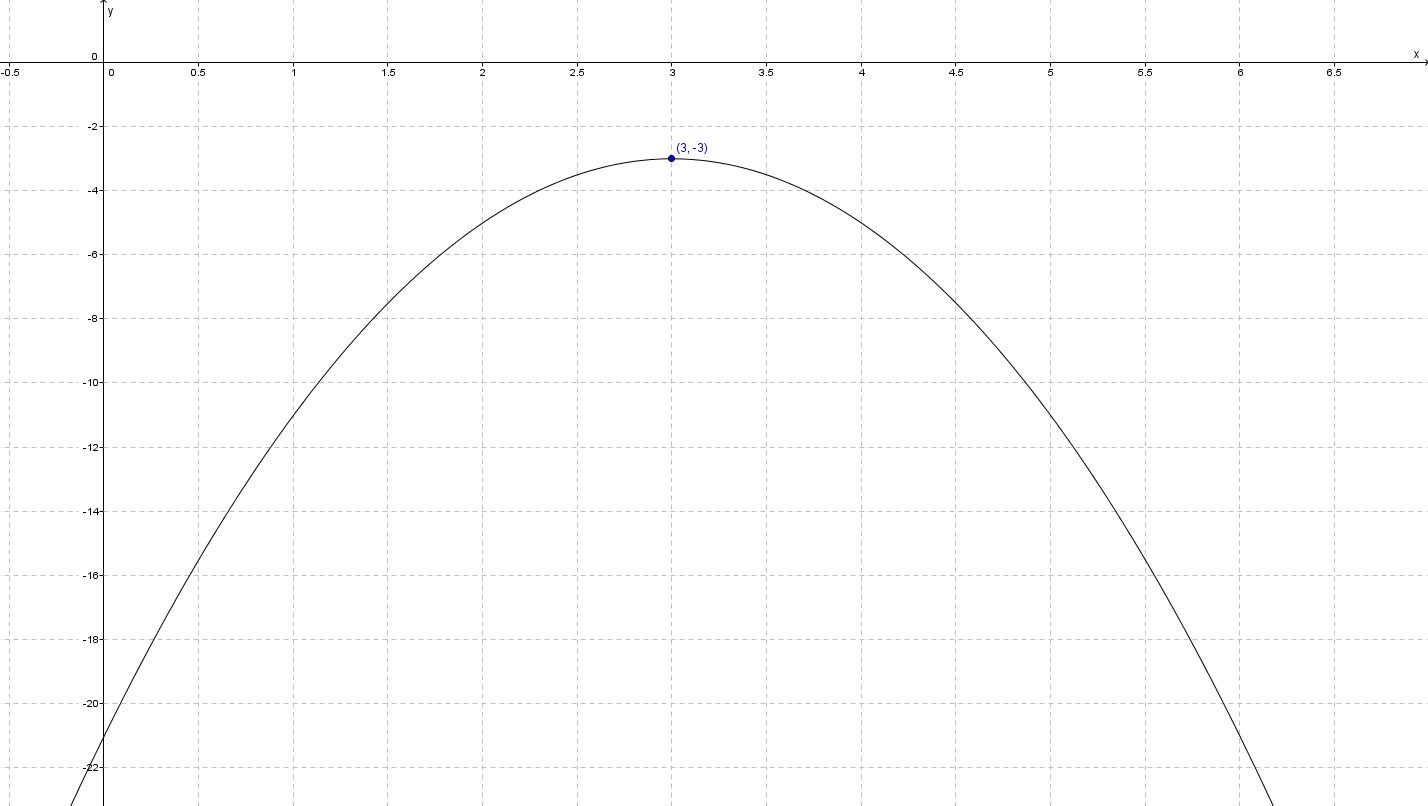
As a hand drawn sketch, this shows all the information we need to sketch the quadratic.

Remember that a parabola is symmetric about its vertex, so all points on one side of the parabola can be reflected across the axis of symmetry to find points on the other side of the parabola. This can help us get even more points to make an even better sketch.
Graph using vertex and x-intercepts
We are able to create a decent graph from the vertex and $y$y-intercept. However, depending on the context of the problem, we may need to know other points on the parabola. It is helpful when graphing to show the vertex along with all intercepts ($x$x and $y$y).
Let's look at an example.
Worked example
Question 1
Consider the quadratic function $f(x)=x^2-2x-3$f(x)=x2−2x−3. Find its vertex and all of its intercepts and create a graph.
Think: When the coefficient of the squared term is positive, the quadratic function has a minimum rather than a maximum. This tells us that the parabola will open upwards. Now we need to find some actual points on the graph.
Do: To find the $y$y-intercept, substitute the value of $0$0 for $x$x in the equation: $f(0)=-0^2-2(0)-3=-3$f(0)=−02−2(0)−3=−3.
We see that the $y$y-intercept is the point $\left(0,2\right)$(0,2).
To find the $x$x-intercepts we need to find where $f(x)=0$f(x)=0. By factoring we get:
| $f(x)$f(x) | $=$= | $x^2-2x-3$x2−2x−3 |
| $=$= | $(x-3)(x+1)$(x−3)(x+1) |
Thus, if $f(x)=0$f(x)=0, we have $x-3=0$x−3=0 or $x+1=0$x+1=0 and so, $x=3$x=3 or $x=-1$x=−1. This means that the coordinates of the $x$x-intercepts are $\left(-1,0\right)$(−1,0) and $\left(3,0\right)$(3,0).
Now we just need to find the vertex. We can do this by completing the square.
| $f(x)$f(x) | $=$= | $x^2-2x-3$x2−2x−3 |
| $=$= | $x^2-2x+1-3-1$x2−2x+1−3−1 | |
| $=$= | $\left(x-1\right)^2-3-1$(x−1)2−3−1 | |
| $=$= | $\left(x-1\right)^2-4$(x−1)2−4 |
Looking at the vertex form we can see that the vertex is $\left(1,-4\right)$(1,−4).
Reflect: Now we can graph the parabola using all of these points that we have found.

Practice questions
Question 2
Consider the quadratic function $y=x^2+2x-8$y=x2+2x−8.
Determine the $x$x-value(s) of the $x$x-intercept(s) of this parabola. Write all answers on the same line separated by commas.
Determine the $y$y-value of the $y$y-intercept for this parabola.
Determine the equation of the vertical axis of symmetry for this parabola.
Find the $y$y-coordinate of the vertex of the parabola.
Draw a graph of the parabola $y=x^2+2x-8$y=x2+2x−8.
Loading Graph...
QUESTION 3
Consider the graph of the parabola below.
Find the $x$x values of the $x$x-intercepts of the parabola. Write all solutions on the same line, separating them with a comma.
Find the $y$y value of the $y$y-intercept for this curve.
Find the equation of the vertical axis of symmetry for this parabola.
What are the coordinates of the parabola's vertex?
Vertex: $\left(\editable{},\editable{}\right)$(,)
Which of the following statements are true about this vertex? Select all true statements.
The $x$x value of the vertex is the average of the $x$x values of the two $x$x-intercepts.
AThe vertex is the minimum value of the graph.
BThe vertex is the maximum value of the graph.
CThe vertex lies on the axis of symmetry.
DThe $y$y value of the vertex is the same as the $y$y value of the $y$y-intercept.
E
Question 4
Consider the function $y=\left(x+6\right)^2$y=(x+6)2. Complete the table of values. What is the minimum value of $y$y? What is the $x$x value that corresponds to the minimum $y$y value? Hence state the vertex of the parabola. Vertex $=$=$\left(\editable{},\editable{}\right)$(,) How many units to the left has $y=x^2$y=x2 been translated? $\editable{}$ units Translate the parabola $y=x^2$y=x2 to sketch $y=\left(x+6\right)^2$y=(x+6)2.
$x$x
$-8$−8
$-7$−7
$-6$−6
$-5$−5
$-4$−4
$y$y
$\editable{}$
$\editable{}$
$\editable{}$
$\editable{}$
$\editable{}$
Question 5
A parabola of the form $y=\left(x-h\right)^2+k$y=(x−h)2+k is symmetrical about the line $x=2$x=2, and its vertex lies $6$6 units below the $x$x-axis. Determine the equation of the parabola. Graph the parabola.
Using the vertex formula
As we have seen, the vertex (or turning point) of a parabola can be found very easily when we are able to write the function in the form $y=a(x-h)^2+k$y=a(x−h)2+k where the vertex is $(h,k)$(h,k).
We have also seen that if we are first given the form $y=ax^2+bx+c$y=ax2+bx+c, we can complete the square to turn it into the form $y=a(x-h)^2+k$y=a(x−h)2+k.
But there's another way!
If we want to avoid going through the entire process of completing the square every time we want to find the vertex of a quadratic, we can develop a formula by completing the square for a general quadratic equation.
Let's complete the square for $ax^2+bx+c=0$ax2+bx+c=0.
| $ax^2+bx+c$ax2+bx+c | $=$= | $0$0 | General quadratic equation |
| $\frac{ax^2}{a}+\frac{bx}{a}+\frac{c}{a}$ax2a+bxa+ca | $=$= | $\frac{0}{a}$0a | Divide all terms by $a$a |
| $\left(\frac{ax^2}{a}+\frac{bx}{a}+\left(\frac{b}{2a}\right)^2\right)+\frac{c}{a}$(ax2a+bxa+(b2a)2)+ca | $=$= | $0+\left(\frac{b}{2a}\right)^2$0+(b2a)2 | Add the square of half of the coefficient of $x$x to both sides |
| $\left(\frac{ax^2}{a}+\frac{bx}{a}+\frac{b^2}{4a^2}\right)+\frac{c}{a}$(ax2a+bxa+b24a2)+ca | $=$= | $\frac{b^2}{4a^2}$b24a2 | Simplify the exponents |
| $\left(\frac{ax^2}{a}+\frac{bx}{a}+\frac{b^2}{4a^2}\right)+\frac{c}{a}-\frac{b^2}{4a^2}$(ax2a+bxa+b24a2)+ca−b24a2 | $=$= | $\frac{b^2}{4a^2}-\frac{b^2}{4a^2}$b24a2−b24a2 | Subtract the square of half of the coefficient of $x$x from both sides |
| $\left(x+\frac{b}{2a}\right)^2+\frac{c}{a}-\frac{b^2}{4a^2}$(x+b2a)2+ca−b24a2 | $=$= | $0$0 | Factor the perfect square trinomial in the parentheses. |
Looking at the expression inside the parentheses, we can see the $x$x-value of the turning point or vertex can be found using $x=\frac{-b}{2a}$x=−b2a.
This also happens to be the equation for the axis of symmetry because every quadratic is symmetric about the vertex.
We can continue this proof to derive a similar but more complicated formula for the $y$y-value of the vertex, or we can simply substitute the $x$x-value of the vertex into the original equation to find the $y$y-value.
- Look at the equation in the form $y=ax^2+bx+c$y=ax2+bx+c
- Identify the $a$a and the $b$b value
- Substitute them into the formula $x=\frac{-b}{2a}$x=−b2a to find the $x$x value of the vertex
- To find the $y$y value of the vertex, use the $x$x value just found and substitute it into the original equation of the parabola
Worked Examples
Question 6
Consider the function $P\left(x\right)=x^2-4x+2$P(x)=x2−4x+2.
Find the $x$x-coordinate of the vertex.
Find the $y$y-coordinate of the vertex.
Graph the function.
Loading Graph...
Question 7
Consider the function $y=x^2+4x+3$y=x2+4x+3.
Determine the equation of the axis of symmetry.
Hence determine the minimum value of $y$y.
Hence state the coordinates of the vertex of the curve.
Here is the graph of another quadratic function. State the coordinates of its vertex.
Loading Graph...What is the relationship between the graph of $y=x^2+4x+3$y=x2+4x+3 and the graph provided?
Select all that apply.
They have the same $x$x-intercepts.
AThey share the same turning point.
BThey have the same concavity.
C