1.09 Integers in the coordinate plane

Quadrant 1 of the coordinate plane

The grid reference system often used in street directories and maps makes use of ordered pairs of numbers, or sometimes letter-number pairs, to describe different regions within an area.

In mathematics, the coordinate plane is used to describe the location of actual points, not regions, in a two-dimensional space. These points are labeled by an ordered pair of numbers of the form $\left(x,y\right)$(x,y), called coordinates.

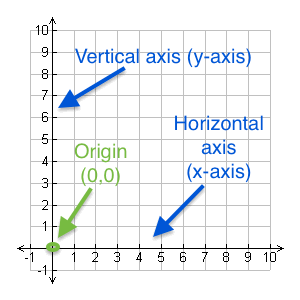
We can think of the coordinate plane as being built from two separate number lines. The first number line we lay down horizontally on the plane. This line is called the $x$x-axis, and for every point in the plane we can talk about its $x$x-coordinate, which is its horizontal position along this axis.

The second number line is placed in a vertical direction, perpendicular to the first number line. This vertical line is called the $y$y-axis, and every point in the plane has a $y$y-coordinate, which is its vertical distance along this axis.

The point at which the $x$x-axis and the $y$y-axis intercept is called the origin. The coordinates of the origin are $\left(0,0\right)$(0,0).

Use the applet below to see how drawing a coordinate plane over an area can be used to describe the location of different objects.

The coordinates of a point are given with respect to the origin. In the image above, we can see that the cat is $6$6 units to the right of the origin, and $2$2 units above the origin. So we can say the cat has the coordinates $\left(6,2\right)$(6,2). The $x$x-coordinate is $6$6 and the $y$y-coordinate is $2$2.

Notice that it would be incorrect to say the cat has the coordinates $\left(2,6\right)$(2,6). These coordinates refer to the point $2$2 units to the right of the origin, and $6$6 units above the origin. The order of the numbers is important!

Worked examples

Question 1

Consider the point $A$A plotted on the coordinate plane. What are the coordinates of point $A$A?

Think: We want to start at the origin and move right/left and up/down to get to point $A$A. 

Do: 
Starting at the origin, we can move $5$5 units across to the right along the $x$x-axis until point $A$A is directly above us. This means that the $x$x-coordinate of point $A$A is $5$5. Next, we will need to move $4$4 units up in the vertical direction to get to $A$A, so the $y$y-coordinate of point $A$A is $4$4. We write the coordinates as $\left(5,4\right)$(5,4).

 

 

 

Practice questions

Question 2

Question 3

Question 4

 

All quadrants of the coordinate plane

We can build the coordinate plane using two copies of the number line to describe the location of shapes and points in a 2D space.

Now we can extend this coordinate system using directed numbers, which will allow us to describe the location of points in any direction from the origin.

The applet below demonstrates the main features of this extended coordinate plane. Each axis now has positive and negative numbers, and this means we can talk about four distinct regions of the plane, called quadrants.

Notice that the 1st quadrant in the top right is equivalent to the coordinate plane that we looked above. The $x$x-coordinate and $y$y-coordinate of a point in the 1st quadrant are both positive.

Moving around counterclockwise we cover the other three quadrants, which have the following features:

• 2nd quadrant: $x$x-coordinates are negative, $y$y-coordinates are positive
• 3rd quadrant: both coordinates are negative
• 4th quadrant: $x$x-coordinates are positive, $y$y-coordinates are negative

Points that lie on an axis, like $\left(-5,0\right)$(−5,0) or $\left(0,4\right)$(0,4), are not in any quadrant.

The advantage of using directed numbers on the coordinate plane is that we no longer have boundaries for the coordinates. If an object begins at some point on the plane, we can move it any which way we like, as far as we like, and still be able to describe its location with respect to the origin.

 

Worked example

Question 5

Consider the point $Q$Q plotted on the coordinate plane.

 

a) What are the coordinates of $Q$Q?
Think: To find the $x$x-coordinate we can draw a vertical line from $Q$Q and read off the number at the point where this line touches the $x$x-axis (the horizontal axis). Similarly, we can find the $y$y-coordinate by drawing a horizontal line from $Q$Q and reading the number at the point where this line intercepts the $y$y-axis (the vertical axis).

Do: The $x$x-coordinate is $-4$−4 and the $y$y-coordinate is $3$3. So the coordinates of $Q$Q are $\left(-4,3\right)$(−4,3).

b)  What quadrant is $Q$Q in?
Think: In the previous part we found that $Q$Q has a negative $x$x-coordinate and a positive $y$y-coordinate.

Do: This means that it is in the 2nd quadrant (Quadrant II), in the top left of the coordinate plane.

 

Practice questions

Question 6

Question 7

Question 8