Borrowing money from the bank to buy a car or a house usually means getting a reducing balance loan. The most common reducible balance loan type is a mortgage. This is when we borrow money to buy a property.
This is the sort of loan where we are charged compound interest as the fee for borrowing money, and at regular time periods, usually months, we are required to make repayments to the financial institution to slowly pay off the loan. The repayments are usually all the same amount, except for the last repayment which is often less than the full amount. Interest is still charged on this final repayment.
When we make each repayment the amount owed (the balance) reduces, hence the name for this type of loan.
As well as calculating the length of time it takes to pay off a loan, we are often interested in the total amount paid on the loan and the total amount of interest paid to the bank.
Analysing a reducing balance loan with a table
Worked examples
example 1
Mr and Mrs Roberts take out a mortgage to purchase a house. They borrow $\$550000$$550000 from a bank that charges them $5.8%$5.8% interest per annum, compounded monthly. At the end of each month the Roberts make a repayment of $\$3500$$3500.
We can represent this situation using a table of values or a spreadsheet. The first and last months of the loan are shown below.
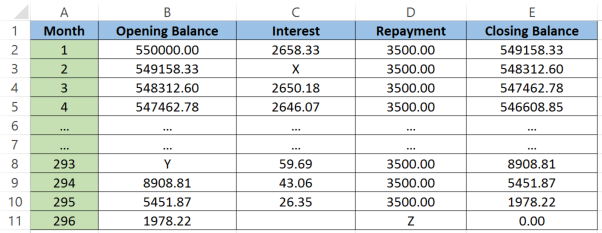
Note the calculation used to create this spreadsheet
- In cell B3, opening balance = closing balance for previous month
- In cell C2, monthly interest = annual rate/12 * opening balance
- In cell D2, repayment = fixed amount (except for last month)
- In cell E2, closing balance = opening balance + interest - repayment
(a) Calculate the value of X in the table.
Think: X is situated in the interest column, so we need to find the interest on the amount at the start of month $2$2. We must first divide the interest rate by $12$12 as interest is calculated monthly.
Do:
$X=\frac{0.058}{12}\times549158.33$X=0.05812×549158.33
$X=2654.26$X=2654.26
(b) Calculate the value of Y in the table.
Think: Usually finding the opening balance is easy because it's the same as the closing balance from the previous time period. But we can't see it in this case. So we'll need to work backwards by writing an equation and solving it.
The equation is opening balance + interest - payment = closing balance.
Do:
$Y+56.59-3500=8908.81$Y+56.59−3500=8908.81
$Y=12349.12$Y=12349.12
(c) Calculate the value of Z in the table.
Think: This is the month where the Roberts will crack open a bottle of champagne since they've finally paid off their loan! Their final repayment will be less than their usual amount. It will be equal to the amount owing at the end of the second last month plus the interest on the amount owing.
Do:
$Z=1978.22+\frac{0.058}{12}\times1978.22$Z=1978.22+0.05812×1978.22
$Z=1987.78$Z=1987.78
(d) Calculate the total repayments made by the Roberts.
Think: The Roberts have made $295$295 repayments each of $\$3500$$3500 plus the final repayment of $\$1987.78$$1987.78
Do: Total repayments = $295\times3500+1987.78$295×3500+1987.78
Total repayments = $\$1034487.78$$1034487.78
(e) Hence determine the total interest the Roberts paid for the loan.
Think: The total interest paid on the loan is their total repayments minus the amount they borrowed.
Do: $1034487.78-550000$1034487.78−550000=$\$484487.78$$484487.78
So you can see that they nearly paid double the purchase price over the $296$296 months, or $25$25 years.
Reflect: How could they pay off their house sooner?
They could try to do one or both of the following:
- Halve the monthly payment and make this new payment fortnightly. This saves a significant amount as they will effectively be making an extra month's payment per year and will pay the loan off sooner. They would end up making an extra repayment each year since there are $26$26 fortnights in a year and$\frac{26}{2}=13$262=13 so they would have paid for $13$13 months instead of $12$12.
- Increase the amount they repay. Intuitively, if you make larger repayments each month or fortnight, you'll be able to pay off your loan sooner, saving you a lot of interest and thus helping you pay less overall.
Total amount paid = total of full repayments + last repayment + interest on last repayment
Total interest paid = total amount paid - initial amount borrowed
Practice question
Question 1
Ivan takes out a car loan for $\$24000$$24000. He is charged $8.1%$8.1% per annum interest, compounded monthly. Ivan makes repayments of $\$450$$450 at the end of each month.
Complete the values in the empty cells in the table below. Give your answers correct to the nearest cent.
Month Opening Balance Interest Repayment Closing Balance 1 $24000$24000 $162.00$162.00 $450$450 $23712.00$23712.00 2 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ 3 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$
Modelling a reducing balance loan with a recurrence relation
Since a reducing balance loan uses compound interest as well as making regular repayments, this type of recurrence relation involves a first order linear recurrence relation.
For a principal loan, $P$P, at the compound interest rate of $r$r per period and a payment of $d$d per period, the sequence of the value of the loan over time forms a first order linear recurrence.
The sequence which generates the value, $V_n$Vn, of the loan at the end of each instalment period is:
- Recursive sequence:
$V_n=V_{n-1}\times(1+r)-d$Vn=Vn−1×(1+r)−d, where $V_0=P$V0=P
- Recursive sequence:
$V_n=V_{n-1}\times(1+r)-d$Vn=Vn−1×(1+r)−d, where $V_1=P$V1=P
Worked examples
Example 2
Tim is starting up his own small business. He has saved $\$15000$$15000 to buy equipment and borrows another $\$50000$$50000 from the bank. He is charged interest at a rate of $4.5%$4.5% per annum, compounded monthly, and he makes monthly repayments of $\$400$$400.
(a) How much does Tim owe at the end of the first month?
Think: Starting from the amount Tim has borrowed, add the interest on and then take away his repayment.
Do:
$\text{Amount owing}=50000+50000\times\frac{0.045}{12}-400=49787.50$Amount owing=50000+50000×0.04512−400=49787.50
So at the end of the first month, Tim owes $\$49787.50$$49787.50.
(b) Write a recurrence relation which gives the balance $B_{n+1}$Bn+1 in terms of $B_n$Bn, and an initial condition $B_0$B0.
Think: Each month there is an increase due to interest (which can be done with a multiplication) and then a decrease due to the repayment. We want $B_1$B1 to be the amount at the end of month $1$1, so we define $B_0=50000$B0=50000.
Do: Using the calculation from part (a), we can see that at any step,
$B_{n+1}=1.00375\times B_n-400$Bn+1=1.00375×Bn−400 ; $B_0=50000$B0=50000
(c) Determine how many months it will take Tim to pay off the loan.
Think: We can enter the recurrence relation into the sequence facility of a calculator, then find the first month in which the balance becomes negative.
Do: For an example showing how to create a table of values for a sequence inspect the first examples given in a previous lesson. Scrolling through your created table you should see the following:
| $n$n | $a_n$an |
|---|---|
| $166$166 | $\$1186.61$$1186.61 |
| $167$167 | $\$791.06$$791.06 |
| $168$168 | $\$394.03$$394.03 |
| $169$169 | $-\$4.49$−$4.49 |
So we can see that Tim pays off the loan in month $169$169.
(d) Calculate the amount of his final repayment.
Think: The amount of the final repayment will be equal to the remaining amount owing in month $168$168, plus the interest generated that month.
Do:
$\text{Final repayment}=394.03+0.00375\times394.03=395.51$Final repayment=394.03+0.00375×394.03=395.51
So the value of the final repayment is $\$395.51$$395.51.
(e) Hence or otherwise, determine the total amount Tim paid for the equipment.
Think: The equipment cost Tim an initial $\$15000$$15000 plus the cost of the loan. The cost of the loan was $168$168 repayments of $\$400$$400 each, plus one final repayment of $\$395.51$$395.51.
Do:
| Total amount paid | $=$= | $15000+168\times400+395.51$15000+168×400+395.51 |
| $=$= | $82595.51$82595.51 |
So the total amount Tim paid is $\$82595.51$$82595.51.
Practice question
Question 2
Bart borrows $\$61000$$61000 from a banking institution. He is charged $6.6%$6.6% per annum interest, compounded monthly. At the beginning of each month, before interest is charged, he makes a repayment of $\$400$$400.
Fill in the missing values in the table. Give all values correct to the nearest cent and use your rounded answers for all subsequent calculations in the table.
Month Opening Balance Repayment Interest Closing Balance 1 $61000$61000 $400$400 $333.30$333.30 $60933.30$60933.30 2 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ 3 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ 4 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Write a recursive rule that gives the closing balance, $B_n$Bn, at the end of month $n$n.
Write both parts of the rule (including for $B_0$B0) on the same line, separated by a comma.
Use your calculator to determine how much is owing on the loan after $4$4 years.
Give your answer to the nearest cent.
At the end of which year and month will the loan have been repaid?
$\editable{}$ year(s) $\editable{}$ month(s)
Reducing balance loans using the CAS financial application
Often it's more convenient to analyse various situations for a reducible balance loan using the financial facility of our calculator. Always remember to write down the values you are using as your working out.
Worked example
example 3
Audrey takes out a car loan for $\$24000$$24000. The finance company charge her $8.5%$8.5% interest compounded monthly.
How much should Audrey repay each month if she wants to repay this loan in $5$5 years?
Using the financial application on our CAS we'd fill it in as follows:
| Compound Interest | ||
|---|---|---|
| N | $60$60 | Number of payments is 60 as 5 years = 60 months |
| I% | $8.5$8.5 | The annual interest rate |
| PV | $24000$24000 | PV is positive as the bank is giving Audrey money |
| PMT | ||
| FV | $0$0 | The future balance will be zero. |
| P/Y | $12$12 | 12 payments per year |
| C/Y | $12$12 | Compounding monthly |
Solving we get: PMT = $-492.40$−492.40
So Audrey should pay $\$492.40$$492.40 each month. Note that PMT displays as a negative number since the payments will be made from Audrey to the financial institution.
Final payment using CAS financial application
Example 4
Audrey takes out a car loan for $\$24000$$24000. The finance company charge her $8.5%$8.5% interest compounded monthly. Audrey decides she can only afford to pay $\$480.00$$480.00 each month which means it will take her a little more than $5$5 years to pay off the loan. Calculate the amount of Audrey's final payment on the loan.
There are two methods in which a final payment can be calculated.
Method 1:
Think: Calculate the amount owing for the final month and increase this by the monthly interest rate.
Do: First find the number of whole payments it will take.
| Compound Interest | ||
|---|---|---|
| N | Number of payments is unknown |
|
| I% | $8.5$8.5 | The annual interest rate |
| PV | $24000$24000 | PV is positive as the bank is giving Audrey money |
| PMT | $-480$−480 | PMT is negative as Audrey is giving money to the bank |
| FV | $0$0 | The future balance will be zero. |
| P/Y | $12$12 | 12 payments per year |
| C/Y | $12$12 | Compounding monthly |
Solving for N we find the number of months to pay the loan is $61.94$61.94. therefore it will take $61$61 full payments of $\$480.00$$480.00 plus a smaller final part payment.
Now find the balance remaining after $61$61 whole payments. Put N = $61$61 and solve for FV. We find that FV = $-449.38$−449.38.
Add the monthly interest to this final balance $\text{Final payment}=449.38+449.38\times0.085\div12=452.56$Final payment=449.38+449.38×0.085÷12=452.56
The final payment is $\$452.56$$452.56
Method 2:
Think: Calculate the FV for the month in which the loan will be paid. This will be an overpayment. Subtract the overpayment amount from the usual monthly payment.
Do: Calculate the FV balance for N = $62$62 months. The FV is $27.44$27.44.
Subtracting $27.44$27.44 from the usual payment gives $\text{Final payment}=480-27.44=452.56$Final payment=480−27.44=452.56
The final payment is $\$452.56$$452.56
Practice question
Question 3
Mr and Mrs Gwen held a mortgage for $25$25 years. Over that time they made monthly repayments of $\$4500$$4500 and were charge a fixed interest rate of $4.4%$4.4% per annum, compounded monthly.
We will use the financial solver on your CAS calculator to determine how much they initially borrowed.
Which variable on the CAS calculator do we want to solve for?
PVAI%BNCPmtDFVEFill in the value for each of the following:
N:$\editable{}$I%:$\editable{}$Pmt:$\editable{}$FV:$\editable{}$PpY:$\editable{}$CpY:$\editable{}$Hence, state how much Mr. and Mrs. Gwen initially borrowed, correct to the nearest dollar.
What if number of payments $\ne$≠ number of compounding periods?
In real life, banks usually calculate interest on loan accounts monthly but people can choose to make fortnightly or even weekly repayments.
When the number of payments is not equal to the number of compounding periods the financial application of the calculator is a great tool.
N is the total number of payments $=\text{payments per year}\times\text{number of years}$=payments per year×number of years
P/Y is number of payments per year
C/Y is the number of times interest is calculated per year
Select the brand of calculator you use below to work through an example involving a reduce balance loan with differing payment and compound periods.
Casio Classpad
How to use the CASIO Classpad to complete the following tasks involving a reducing balance loan using the inbuilt financial solver.
A couple borrow $\$550000$$550000 to buy a house. The bank offers a reducing balance loan with an interest rate of $2.85%$2.85% p.a. compounded monthly. The couple opt to make fortnightly payments of $\$1200$$1200 in order to pay off the loan.
Assume there are $26$26 fortnights in a year.
Find the balance of the loan after two years.
How many years will it take the couple to pay off the loan? (Round your solution to one decimal place.)
TI Nspire
How to use the TI Nspire to complete the following tasks involving a reducing balance loan using the inbuilt financial solver.
A couple borrow $\$550000$$550000 to buy a house. The bank offers a reducing balance loan with an interest rate of $2.85%$2.85% p.a. compounded monthly. The couple opt to make fortnightly payments of $\$1200$$1200 in order to pay off the loan.
Assume there are $26$26 fortnights in a year.
Find the balance of the loan after two years.
How many years will it take the couple to pay off the loan? (Round your solution to one decimal place.)
Practice question
Question 4
Valerie borrows $\$345000$$345000 to buy an apartment. The bank offers a reducing balance loan with an interest rate of $2.35%$2.35% p.a. compounded monthly. Valerie opts to make fortnightly payments of $\$1250$$1250 in order to pay off the loan. Use the financial application on your calculator to answer the following questions.
Assume there are $26$26 fortnights in a year.
What is the balance, in dollars, after $100$100 weeks?
Round your answer to the nearest cent.
Approximate how long it takes her to pay off the loan in years.
Round your answer to two decimal places.