We will start this lesson by exploring some situations that can be represented by graphs or networks.
Example 1
Here is a map that shows how the capital cities and some country towns in Australia are connected by the road network. The map shows the major roads connecting these cities together as undirected edges (since we can travel in both directions on these roads).

Now we can get rid of the underlying map, and are left with the connections between the capital cities as a network:

If we only care about if we can get from one city to another, and not how far it is between the cities, we can simplify the network a lot:

Although a lot of detail is removed, we can easily see all kinds of information. For example:
- You can’t drive straight from Canberra to Perth without going through at least one other capital city along the way.
- If you’re in Hobart you can drive around but you’re never going to reach any other capital city.
- If you want to go from Melbourne to Sydney you can go through Canberra or you can drive around it.
Our network is not drawn to scale like the map, but that’s okay - here we are only interested in whether cities are connected. When it is needed, we can use a weighted graph to represent scale.
EXAMPLE 2
You will see this kind of network all around you once you know how to look for it. For example, here is the London tube map as a network:
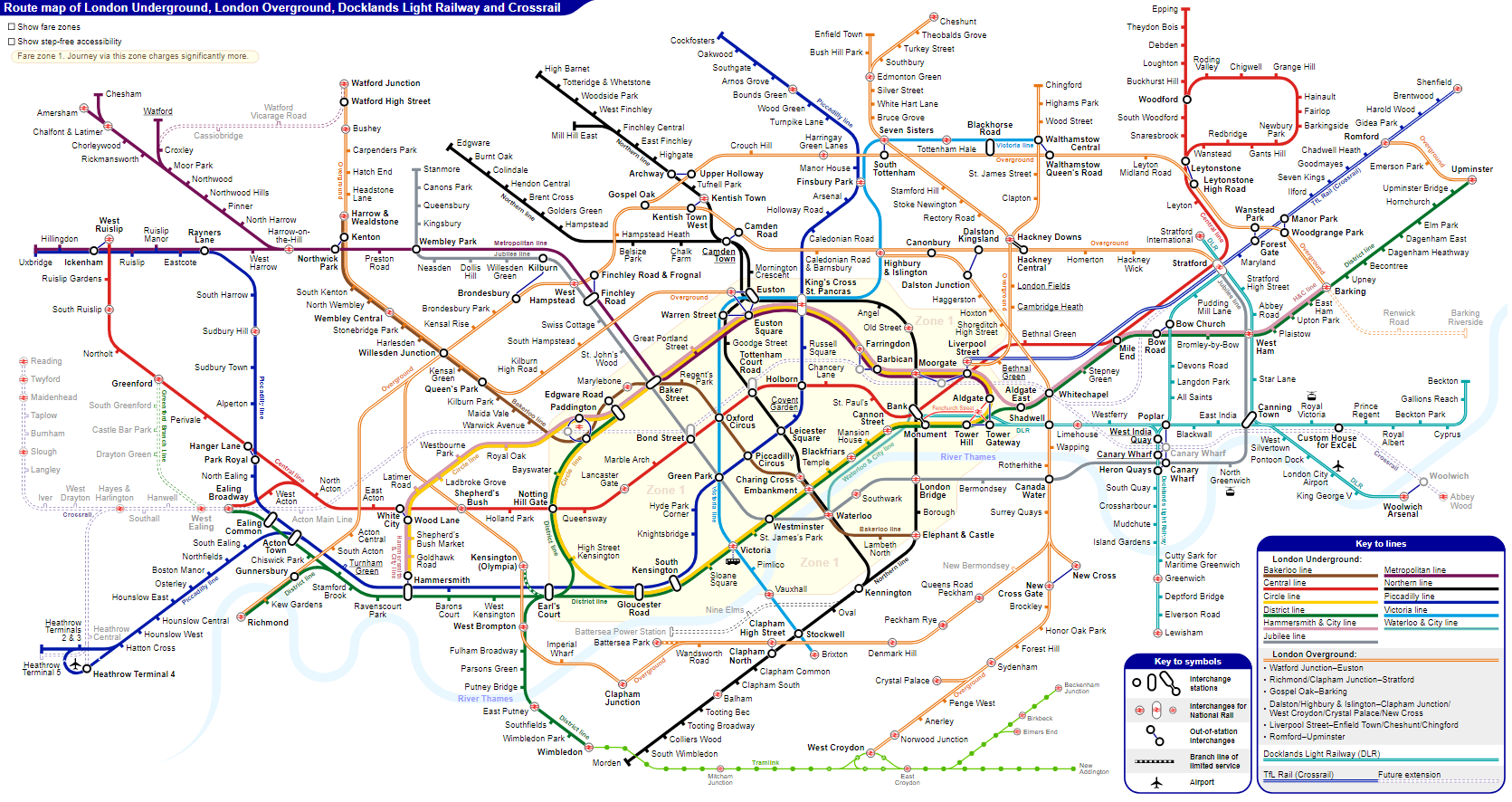
By sacrificing realism and only representing the information we care about (which stations are connected to which other stations and how), using the map becomes easier.
EXAMPLE 3
This next network is a completely different application. This is the family tree for King Charles II of Spain:
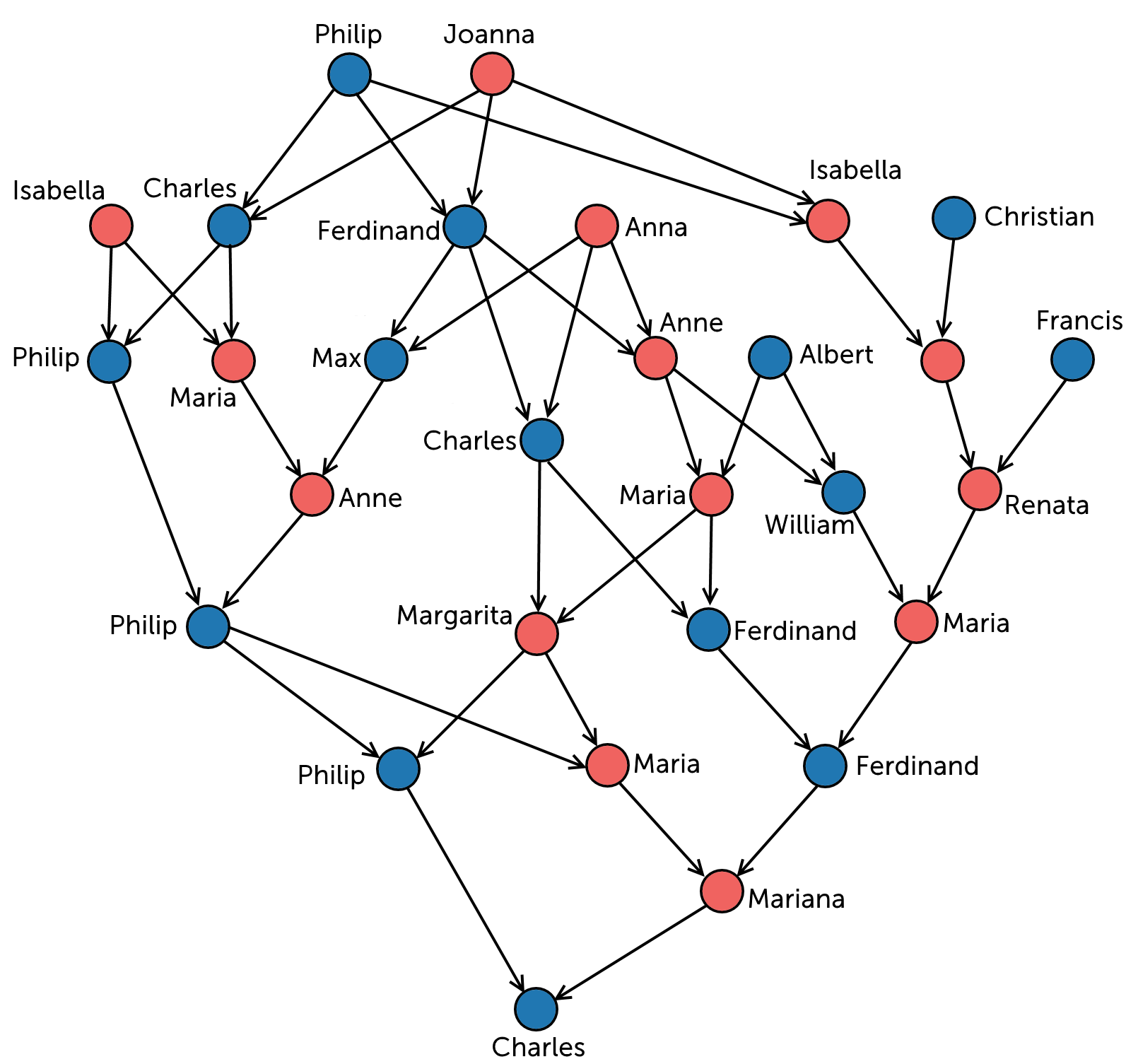
Note that the edges have arrows this time to show who is the parent and who is the child, so this is a directed network. There are seven vertices that don’t have any arrows pointing at them, and every other vertex has exactly two edges pointing at them, one for their mother and one for their father.
Practice questions
Question 1
The following figure displays newspaper routes between several houses.

The vertices are:
The houses
AThe space enclosed by the routes
BThe routes
CHow many vertices are there?
How many edges are there?
Question 2
A beach volleyball social competition team can have 3 players on the court at any time. The team has 5 players at the tournament. The table shows 3 combinations that the coach has already used in the first three games.
| Game | Players chosen |
|---|---|
| 1 | Ryan, Jimmy, Lucy |
| 2 | Lucy, Beth, Ellie |
| 3 | Ellie, Ryan, Jimmy |
Which of the following graphs shows the combinations of players that have already played together?
 A
A B
B C
C D
DThere is one more game left in the tournament.
Who should the coach choose to play so that every team member has played with every other team member at least once?
Beth
AJimmy
BLucy
CRyan
DEllie
E
Question 3
The following table lists the amount of time it takes to queue up for three rides at an amusement park, and the amount of time it takes to travel between them:
| Carousel | Pirate Ship | Haunted House | |
| Carousel | $3$3 | $5$5 | $4$4 |
| Pirate Ship | $5$5 | $13$13 | $6$6 |
| Haunted House | $4$4 | $6$6 | $11$11 |
Represent this information using a network.
Adjacency matrices for undirected networks
It is sometimes useful to use an adjacency matrix to represent a network. This is a square matrix of numbers, with a row and a column for each vertex, that records how many connections there are between the vertices. For an undirected network, the entry for a particular row and column represents the number of edges connecting the matching vertices.
EXAMPLE 4
Here’s a simple network (no loops and no multiple edges) with $5$5 vertices:

Now we can create a matrix, with a row and a column for each vertex:

Then we put the number edges connecting two vertices as the corresponding table entry. Let’s start by filling out the first row by putting a $1$1 if it is connected to $A$A, and a $0$0 if it isn’t.

$0$0 comes first because $A$A isn’t connected to itself (there’s no loop at $A$A), and $A$A is connected to $B$B, $C$C, $D$D, and $E$E, so we put a $1$1 for each other entry in the table.
Since these edges are undirected, we can fill out the first column with the same numbers - if $A$A is connected to $B$B, then $B$B is connected to $A$A, and so on:

Now to fill out the second row, we notice that $B$B is connected to $A$A (already recorded), not itself (no loop), and it is connected to $C$C, $D$D, and $E$E:

We then record the remaining connections between $C$C, $D$D, and $E$E in the same way:

In the completed matrix, notice that:
- The diagonal running top-left to bottom-right (called the main diagonal) has only $0$0's.
This indicates that no edge is connected to itself in the network - there are no loops. - The numbers off the main diagonal are only $0$0’s and $1$1’s.
This indicates that there are no multiple edges.
All adjacency matrices representing simple networks will have these features.
As an added bonus, for a network with no loops, the sum of all the entries in a row (or column) gives us the degree of the corresponding vertex - we can tell from the table that $C$C and $E$E have degree $2$2, $D$D has degree $3$3, and $A$A and $B$B have degree $4$4.
Adjacency matrices for directed networks
Now for a directed network, the entry in a particular row and column indicates the number of edges going from the corresponding row vertex to the corresponding column vertex.
EXAMPLE 5
Here’s a directed, non-simple network with $5$5 vertices and its corresponding adjacency matrix:

This matrix looks a little different from the last one. Notice that:
- The matrix is not symmetrical across the main diagonal (an edge from $A$A to $B$B can exist without an edge from $B$B to $A$A),
- There is a $1$1 on the main diagonal because it is not a simple graph as there is a loop at $C$C, and
- There’s a $2$2 in the table because there are two edges from $D$D to $E$E.
While an asymmetrical matrix means the network is directed, there are directed networks that will produce a symmetrical adjacency matrix.
For directed networks, we can add all of the elements in the adjacency matrix to determine the number of edges on the graph.
When a network contains loops, there will be non-zero values on the main diagonal of the adjacency matrix. Each loop is counted as the vertex as having one connection to itself.
When we calculate the degree of a vertex by adding the elements in a row (or column) of the adjacency matrix, numbers on the main diagonal need to be doubled because loops are counted twice.

In the graph above the degree of vertex $C$C is $4$4, because the loop is considered to be two edges into vertex $C$C. However if we add the numbers in row $C$C of the corresponding adjacency table we only get $3$3. The $1$1 on the main diagonal must be counted twice as it represents the loop at $C$C.
Adjacency matrices for weighted graphs
Adjacency matrices can be used for weighted graphs where each element in the matrix represents the weight assigned to that edge.
EXAMPLE 6
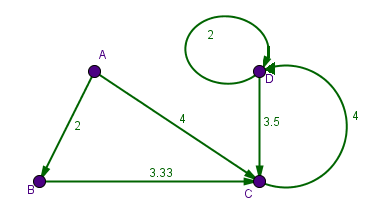
Setting up the matrix template we need, $4$4 vertices means it will be a $4\times4$4×4 matrix.

From vertex $A$A, there are $2$2 edges. The edge connected to $B$B has weight $2$2, and the edge to $C$C has weight $4$4.

From vertex $B$B there is just one edge. It goes to $C$C with weight $3.33$3.33.

From vertex $C$C there is just one edge. It goes to $D$D with weight $4$4.
From vertex $D$D there are two edges. One of them is a loop and this gets written in the $D$D to $D$D position.

Creating a network from an adjacency matrix
If we know that we have a directed or undirected network, the information in the adjacency matrix is enough for us to draw a graph to represent the network.
Example 7
Here’s a table with $6$6 rows and columns (so there are $6$6 vertices in the network), and we are also told that the network is undirected.

This is a representation of the network that we get when we draw it out:

- start with the first row, and the vertex on the left
- draw in the edges connected to that vertex
- move on to the next row/next vertex clockwise, ignoring the numbers below the main diagonal - they get drawn into the network when we do earlier rows for undirected networks. If the graph is directed, all the numbers need to be turned into edges.
- The degree of a vertex is the number of edges connected to that vertex. Loops are counted twice.
- An adjacency matrix is a square array of numbers, a row and a column for each vertex, that records how many connections there are between the vertices.
- For undirected networks, the element for a particular row and column represents the number of edges connecting the matching vertices.
- For directed networks, the element in a particular row and column indicates the number of edges going from the corresponding row vertex to the corresponding column vertex.
- Loops are indicated by elements on the main diagonal with each loop counting as one connection.
Practice questions
Question 4
Fill in the adjacency matrix for this network:

$A$A $B$B $C$C $D$D $A$A $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $B$B $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $C$C $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $D$D $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ What is the degree of vertex $A$A?
Question 5
Fill in the adjacency matrix for this network:

$P$P $Q$Q $R$R $S$S $P$P $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $Q$Q $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $R$R $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $S$S $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ What is the degree of vertex $P$P?
Question 6
Select the network with this adjacency matrix:
|
- ABCDE
Multi-stage connections
The elements in an adjacency matrix for a directed graph represent direct connections from one vertex to another.
For example, the directed graph below can be represented by the adjacency matrix $M$M.
Matrix $M$M shows that there are three one-stage connections from vertex $C$C - one each to vertices $A$A, $B$B and $D$D.
A two-stage connections is a connections between two nodes that goes via some other node. In the given graph, the path $C,A,B$C,A,B is a two-stage path from $C$C to $B$B. There is also a two-stage path $C,A,D$C,A,D from $C$C to $D$D.
The two-stage connections can be seen in the $M^2$M2 matrix, which can be obtained by multiplying the matrix $M$M by itself, either using technology or performing matrix multiplication.

Two-stage connections are indicated by the non-zero elements in $M^2$M2. The two $1$1’s in the matrix indicate there are two 2-step paths from $C$C to $B$B ($CAB$CAB) and from $C$C to $D$D ($CAD$CAD). But how does this method actually work?
Let's consider the entry $3,2$3,2 in the matrix $M^2$M2, which indicates that there is a single 2-step path from $C$C to $B$B. To get this value via matrix multiplication, we need to take the product of the third row of matrix $M$M with the second column of matrix $M$M. Since the third row of matrix $M$M counts the number of paths from $C$C to the other vertices, and the second row counts the number of paths to $B$B from other vertices, multiplying them together is the same as counting "how many paths are there from $C$C to $B$B through one other vertex?".
This use of matrix arithmetic can even be extended to use $M^n$Mn to identify $n$n-stage connections.
For this particular graph, we can see that there are no three-stage connections because $M^3$M3 is a zero matrix. That means there is no way to get to one vertex to another in three steps.
Multi-stage connections can represent numerous practical situations, such as air transport links between cities, the ranking of players in sporting competitions, connections in computer networks and many others.
Practice questions
QUESTION 7
Consider the given graph.
Create the adjacency matrix, $M$M.
$A$A $B$B $C$C $D$D $A$A $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $B$B $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $C$C $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $D$D $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ How many one-stage paths are there between $B$B and $D$D?
Find the second-stage adjacency matrix $M^2$M2 using technology or otherwise.
$A$A $B$B $C$C $D$D $A$A $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $B$B $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $C$C $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $D$D $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ How many two-stage paths are there between $C$C and $D$D?
QUESTION 8
Consider the given graph.
Create the adjacency matrix, $M$M.
$X$X $Y$Y $Z$Z $X$X $\editable{}$ $\editable{}$ $\editable{}$ $Y$Y $\editable{}$ $\editable{}$ $\editable{}$ $Z$Z $\editable{}$ $\editable{}$ $\editable{}$ Find the second-stage adjacency matrix $M^2$M2 using technology or otherwise.
$X$X $Y$Y $Z$Z $X$X $\editable{}$ $\editable{}$ $\editable{}$ $Y$Y $\editable{}$ $\editable{}$ $\editable{}$ $Z$Z $\editable{}$ $\editable{}$ $\editable{}$ How many two-stage paths are there between $Y$Y and $X$X?
There is one two-stage path from $Y$Y to $X$X. What is this path?
Enter each vertex as a capital letter, separated by commas.
Find the third-stage adjacency matrix $M^3$M3 using technology or otherwise.
$X$X $Y$Y $Z$Z $X$X $\editable{}$ $\editable{}$ $\editable{}$ $Y$Y $\editable{}$ $\editable{}$ $\editable{}$ $Z$Z $\editable{}$ $\editable{}$ $\editable{}$ Which vertices are connected by a three-stage path? Give a single example, writing only the start and end vertices.
Enter each vertex as a capital letter, separated by commas.









