8.05 Probability density functions and the normal distribution

The empirical rule and probability

The empirical rule gives us the percentages of scores we can expect to be within $1$1, $2$2 or $3$3 standard deviations of the mean. These percentages also tell us the probability that a score will have a particular $z$z-score. That is, the probability that a score will have:

• a $z$z-score between $-1$−1 and $1$1 is $68%$68%
• a $z$z-score between $-2$−2 and $2$2 is $95%$95%
• a $z$z-score between $-3$−3 and $3$3 is $99.7%$99.7%

The empirical rule can also tell us whether particular scores are unlikely to occur, that is, they are outliers if they have a $z$z-score that is more than $3$3 standard deviations from the mean.

We can use the $z$z-score to help us describe the likelihood of a score being in a particular range. For example, If a score, $x$x, has a $z$z-score of $3$3, the probability of randomly selecting a score less than $x$x is highly likely (by the empirical rule) while the probability of randomly selecting a score greater than $x$x is very unlikely.

Note: We need to be cautious about these probabilities because they are only approximations. Other ways to find the probability is to use technology, such as the desmos normal distribution calculator, or a standard normal distribution table.

The standard normal distribution

When finding probabilities from a continuous probability distribution we were integrating the function to find the area under the probability density function for a specific interval. It's difficult to do the same for a normal distribution because the equation is quite complicated. Instead, we can use technology or a probability table to find the cumulative probability values for a given $z$z-value.

The probability table is developed from the standard normal distribution which is the simplest form of a normal distribution.

The standard normal distribution has three key features:

• its graph is bell shaped
• it has a mean, median and mode of $0$0 (i.e. $\mu=0$μ=0)
• it has a standard deviation of $1$1 (i.e. $\sigma=1$σ=1)

The standard normal distribution is of great interest because any data set with some other normal distribution can be rescaled so that it has the standard normal distribution. This means that we only need to know the properties of the standard normal distribution in order to make predictions about data from infinitely many other normal distributions with a different mean and standard deviation.

The standard normal distribution table

The standard normal distribution table makes it possible to determine this probability in terms of numbers of standard deviations away from the mean (that is, the $z$z-score). In the tables given, the leftmost column labelled $z$z, and the column headings are used to determine the numbers of standard deviations. That is, the leftmost column gives the $z$z-score up to the first decimal place and the column headings designate the second decimal place. The probabilities are in the body of the table.

Only the positive numbers of $z$z-scores need be shown in the table because the distribution is symmetrical. (Half of the probability is on the positive side and half on the negative.)

In short, the table tells us $P\left(Z\le z\right)$P(Z≤z) where $Z$Z is the standard normal variable and $z$z is the standardised score ($z$z-score). It is equivalent to finding the area under the bell curve to the left of $z$z. So to find the probabilities of a particular range of values for a non-standard normally distributed data set, we need to first find the standardised score ($z$z-score) and then use the table.

The cumulative probabilities of the standard normal distribution:

Worked example

Example 1

A data set is normally distributed. Use the table to find:

(a) $P\left(Z\le2\right)$P(Z≤2)

Solution: Look up $z=2$z=2 on left column of the probability table and across to the first column corresponding to $z=2.00$z=2.00. The probability is $0.9772$0.9772.

(b) $P\left(Z\le-2\right)$P(Z≤−2)

Solution: Because the bell curve is symmetrical and the area under the curve is $1$1, the area to the left of $z=-2$z=−2 is equal to the area to the right of $z=2$z=2. Therefore we can simply calculate $1-P\left(Z\le2\right)=1-0.9772=0.0228$1−P(Z≤2)=1−0.9772=0.0228

(c) $P\left(0\le Z\le1\right)$P(0≤Z≤1)

Solution: The probability between $0$0 and $1$1 is equal to the area to the left of $z=1$z=1 take away the area to the left of $z=0$z=0. In other words, $P\left(Z\le1\right)-P\left(Z\le0\right)=0.8413-0.5=0.3413$P(Z≤1)−P(Z≤0)=0.8413−0.5=0.3413

(d) The median

Think: The area either side of the median is $0.5$0.5 therefore we want to find the score with probability $0.5$0.5 in the table, that is $P\left(Z\le z\right)=0.5$P(Z≤z)=0.5

Do: Looking up the table for $0.5$0.5 we see that $z=0$z=0. Therefore the median is $0$0 (which is also the same value as the mean and the mode).

(e) the $3$3rd quartile

Think: The $3$3rd quartile is $0.75$0.75 of the way through data, so we are finding $z$z such that $P\left(Z\le z\right)=0.75$P(Z≤z)=0.75

Do: Looking up the table we see that $0.75$0.75 is close to $P\left(Z\le0.67\right)=0.7486$P(Z≤0.67)=0.7486 and $P\left(Z\le0.68\right)=0.7517$P(Z≤0.68)=0.7517. $z=0.67$z=0.67 is closer to $0.75$0.75 so the $3$3rd quartile is $0.67$0.67.

(f) the $6$6th decile

Think: The $6$6th decile is $0.6$0.6 of the way through the data. Therefore we are finding $z$z such that $P\left(Z\le z\right)=0.6$P(Z≤z)=0.6

Do: Looking up the table for values close to $0.6$0.6 we can see that $P\left(Z\le0.25\right)=0.5987$P(Z≤0.25)=0.5987 and $P\left(Z\le0.26\right)=0.6026$P(Z≤0.26)=0.6026 are close to $0.6$0.6. $z=0.25$z=0.25 is closer to $0.6$0.6, therefore the $6$6th decile is $0.25$0.25.

Example 2

A normally distributed data set has a mean of $6$6 and standard deviation of $2$2. Convert the following probabilities to probabilities involving the standard normal distribution, and then use the empirical rule to find them.

(a) $P\left(X\ge6\right)$P(X≥6)

Solution: $6$6 is the mean of the data set therefore the $z$z-score is $0$0 and $P\left(X\ge6\right)=P\left(Z\ge0\right)$P(X≥6)=P(Z≥0)

According to the empirical rule, $P\left(Z\ge0\right)=0.5$P(Z≥0)=0.5

(b) $P\left(4\le X\le8\right)$P(4≤X≤8)

Solution: For $x=4$x=4, $z=-1$z=−1 as it is $1$1 standard deviation below $6$6.

For $x=8$x=8, $z=1$z=1 as it is $1$1 standard deviation above $6$6.

Therefore $P\left(4\le X\le8\right)=P\left(-1\le Z\le1\right)$P(4≤X≤8)=P(−1≤Z≤1). The empirical rule predicts that $68%$68% of scores lie within $1$1 standard deviation above and below the mean. Therefore, $P\left(-1\le Z\le1\right)=0.68$P(−1≤Z≤1)=0.68

(c) $P\left(X\le10\right)$P(X≤10)

For $x=10$x=10, $z=2$z=2 as $10$10 is $2$2 standard deviations above the mean $(10=6+2+2)$(10=6+2+2).

Therefore $P\left(X\le10\right)=P\left(Z\le2\right)$P(X≤10)=P(Z≤2).

The empirical rule predicts that $95%$95% of scores lie within $2$2 standard deviations above or below the mean. This means that $47.5%$47.5% will lie $2$2 standard deviations above the mean.

Therefore $P(Z\le2)=0.5+0.475=0.975$P(Z≤2)=0.5+0.475=0.975

(d) $P(0\le X\le8)$P(0≤X≤8)

For $x=0$x=0, $z=-3$z=−3 as $0$0 is $3$3 standard deviations below the mean $(0=6-2-2-2)$(0=6−2−2−2).

For $x=8$x=8, $z=2$z=2 (which we know from part (b))

Therefore $P\left(0\le X\le8\right)=P\left(-3\le Z\le2\right)$P(0≤X≤8)=P(−3≤Z≤2)

The empirical rule predicts $99.7%$99.7% of scores are $3$3 standard deviations above and below the mean, therefore $49.85%$49.85% of scores are below the mean. And from part (b) we found that $47.5%$47.5% of scores are above the mean.

Therefore $P\left(-3\le Z\le2\right)=0.4985+0.475=0.9735$P(−3≤Z≤2)=0.4985+0.475=0.9735.

Note: To find this probability using the desmos normal distribution calculator, enter the mean: $u=0$u=0, the standard deviation: $s=1$s=1, the lower limit: $a=-3$a=−3, and the upper limit: $b=2$b=2 , to get  $P\left(-3\le Z\le2\right)=0.9759$P(−3≤Z≤2)=0.9759 as shown below:

Practice questions

question 1

Question 2

Question 3

Exploration: estimating the normal distribution probabilities using the trapezoidal rule

The normal distribution probability density function is given by:

$\phi\left(x\right)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}$ϕ(x)=1σ√2π​e−(x−μ)22σ2​

We can use the trapezoidal rule to approximate the area under the normal curve and hence calculate the probabilities of different outcomes. For example, let's calculate the area or probability of getting up to one standard deviation away from the mean for a normally distributed variable, using the trapezoidal rule. The empirical rule tells us that we approximately $68%$68% of scores are within one standard deviation for a normally distributed variable as shown in the diagram below.

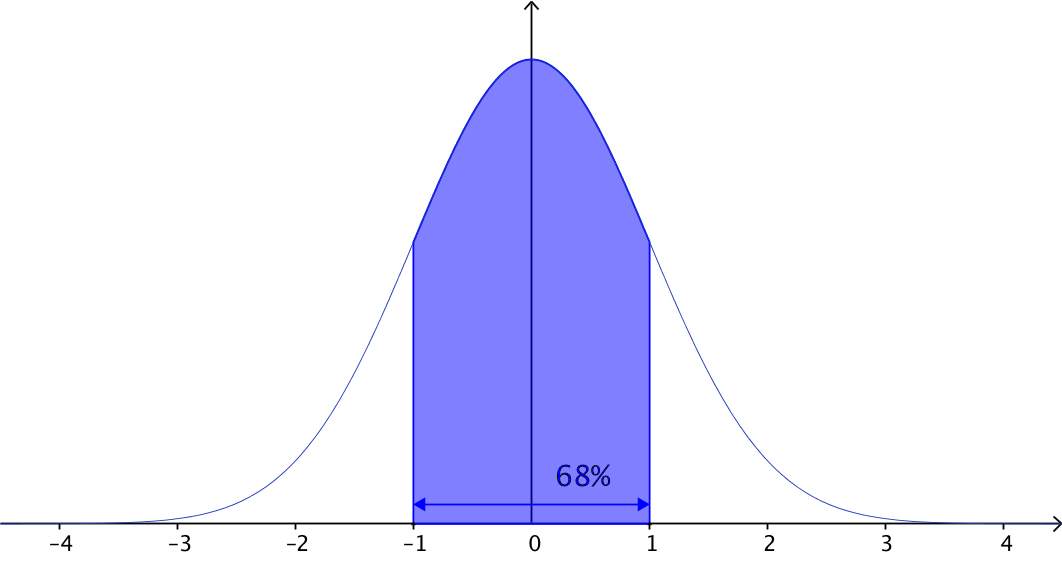
To make the process a bit easier we will use an approximation of the function:

$\phi\left(x\right)=\frac{1}{\sqrt{2\pi}}e^{\frac{-x^2}{2}}$ϕ(x)=1√2π​e−x22​

Let's use the trapezoidal rule with 4 intervals to find the approximate area under the curve between $0$0 and $1$1 standard deviations and double it to account for left and right of the mean.

Therefore $a=0$a=0, $b=1$b=1 and $h=\frac{1--0}{4}=0.25$h=1−−04​=0.25

Completing the table of values:

$x$x	$0$0	$0.25$0.25	$0.5$0.5	$0.75$0.75	$1$1
$\phi\left(x\right)$ϕ(x)	$\frac{1}{\sqrt{2\pi}}e^0$1√2π​e0	$\frac{1}{\sqrt{2\pi}}e^{\frac{-(0.25)^2}{2}}$1√2π​e−(0.25)22​	$\frac{1}{\sqrt{2\pi}}e^{\frac{-(0.5)^2}{2}}$1√2π​e−(0.5)22​	$\frac{1}{\sqrt{2\pi}}e^{\frac{-(0.75)^2}{2}}$1√2π​e−(0.75)22​	$\frac{1}{\sqrt{2\pi}}e^{\frac{-1}{2}}$1√2π​e−12​
$\phi\left(x\right)$ϕ(x)	$0.399$0.399	$0.387$0.387	$0.352$0.352	$0.301$0.301	$0.242$0.242

 

Substituting into the general trapezoidal formula:

$\int_a^b\ f\left(x\right)$∫ba​ f(x)	$\approx$≈	$\ \frac{h}{2}\left[f\left(a\right)+f\left(b\right)+2\left(f\left(x_1\right)+f\left(x_2\right)+\dots+f\left(x_{n-1}\right)\right)\right]$ h2​[f(a)+f(b)+2(f(x1​)+f(x2​)+…+f(xn−1​))]
	$\approx$≈	$\frac{0.25}{2}\left[f\left(0\right)+f\left(1\right)+2\left(f\left(0.25\right)+f\left(0.5\right)+f\left(0.75\right)\right)\right]$0.252​[f(0)+f(1)+2(f(0.25)+f(0.5)+f(0.75))]
	$\approx$≈	$\frac{0.25}{2}\left[0.399+0.242+2\left(0.387+0.352+0.301\right)\right]$0.252​[0.399+0.242+2(0.387+0.352+0.301)]
	$\approx$≈	$0.340$0.340

 

Doubling this to account for left and right of the mean, we get $0.68$0.68 which is the same as our empirical approximation.