5.01 Arithmetic sequences

Definition of a sequence

An ordered collection of numbers or objects is called a sequence or progression. It is similar to a set, but it may contain repetition and its order is important. If the sequence ends, it is known as a finite sequence. Otherwise, it is said to be infinite. For example $−3,5,13,21$−3,5,13,21... and $1,10,100,1000$1,10,100,1000... are examples of mathematical sequences. The "..." at the end of each denotes that these sequences are infinite.

Common difference and the first term

A sequence in which each term changes from the last by adding a constant amount is called an arithmetic sequence. We refer to the constant the terms are changing by as the common difference, which will result from subtracting any two successive terms $\left(T_n-T_{n-1}\right)$(Tn​−Tn−1​). $T_n$Tn​ is known as the $n$nth term and $T_{n-1}$Tn−1​ is the term directly preceding it.

The first sequence written above $-3,5,13,21,\ldots$−3,5,13,21,… is an arithmetic sequence with a common difference of $8$8. On the other hand, the second sequence $1,10,100,1000,\ldots$1,10,100,1000,… is not arithmetic because the difference between each term is not constant.

The common difference is very important in defining our sequence, but we need one extra piece of information to know exactly what numbers we are dealing with–we need to know where the sequence starts. We denote the first term by the letter $a$a and the common difference by the letter $d$d. We know each term differs from the previous one by $d$d, since, $T_2=T_1+d$T2​=T1​+d, $T_3=T_2+d$T3​=T2​+d and so on.

Recurrence relation

A recurrence relation is an equation that defines a sequence based on a rule that gives the next term as a function of the previous term (or terms). So, we can write any arithmetic sequence as the recurrence relation:

$T_n=T_{n-1}+d,T_1=a$Tn​=Tn−1​+d,T1​=a

A recurrence relation is a very straight forward way of describing the sequence, but it isn't very helpful for finding specific terms. For example, if we wanted to find $T_{100}$T100​, we would have to list out every single term so that we could get to the point where we find:

$T_{100}=T_{99}+d$T100​=T99​+d

Explicit formula

We can, in fact, find an explicit formula written solely in terms of $a$a and $d$d. This is useful for finding the $n$nth term without listing the sequence in full.

Let's look at a table of a concrete example to see the pattern for the explicit formula. Returning to the sequence $-3,5,13,21,\ldots$−3,5,13,21,…, we have $a=-3$a=−3 and $d=8$d=8.

$n$n	$T_n$Tn​	Pattern
$1$1	$-3$−3	$-3$−3
$2$2	$5$5	$-3+8$−3+8
$3$3	$13$13	$-3+2\times8$−3+2×8
$4$4	$21$21	$-3+3\times8$−3+3×8
...
$n$n	$T_n$Tn​	$-3+(n-1)\times8$−3+(n−1)×8

The pattern starts to become clear and we could guess that the tenth term becomes:

$T_{10}=69=-3+9\times8$T10​=69=−3+9×8

And the one-hundredth term:

$T_{100}=789=-3+99\times8$T100​=789=−3+99×8

And following the pattern, the explicit formula for the $n$nth term is:

$T_n=-3+(n-1)\times8$Tn​=−3+(n−1)×8

We could create a similar table for an arithmetic progression with starting value $a$a and common difference $d$d and we would observe the same pattern. Hence, the general rule for finding the the $n$nth term of any arithmetic sequence is given by:

$T_n=a+\left(n-1\right)d$Tn​=a+(n−1)d

Worked examples

Example 1

For the sequence $87,80,73,66...$87,80,73,66..., find an explicit rule for the $n$nth term and hence, find the $30$30th term.

Think: Check that the sequence is arithmetic, does each term differ from the last by a constant? Then write down the starting value $a$a and common difference $d$d and substitute these into the general form: $T_n=a+(n-1)d$Tn​=a+(n−1)d

Do: Each term decreases from the last by $7$7. So we have an arithmetic sequence with: $a=87$a=87 and $d=-7$d=−7. The general formula for this sequence is:

$T_n=87+\left(n-1\right)\times\left(-7\right)$Tn​=87+(n−1)×(−7) or $T_n=87-7(n-1)$Tn​=87−7(n−1)

Hence, the $30$30th term is:

$T_{30}=87-7\times29=-116$T30​=87−7×29=−116

Example 2

If an arithmetic sequence has $T_5=38$T5​=38 and $T_9=66$T9​=66, find the recurrence relation for the sequence.

Think: To find the recurrence relation we need the starting value and common difference. As we have two terms we can set up two equations in terms of $a$a and $d$d using $T_n=a+(n-1)d$Tn​=a+(n−1)d, which applies to any term of an arithmetic sequence.

Do:

$T_5$T5​:

$a+4d=38$a+4d=38

$.....\left(1\right)$.....(1)

and

$T_9$T9​:

$a+8d=66$a+8d=66

$.....\left(2\right)$.....(2)

If we now subtract equation $\left(1\right)$(1) from equation $\left(2\right)$(2) the first term in each equation will cancel out to leave us with:

$\left(8d-4d\right)$(8d−4d)	$=$=	$66-38$66−38
$4d$4d	$=$=	$28$28
$\therefore d$∴d	$=$=	$7$7

With the common difference found to be $7$7, we can substitute this back into the equation $\left(1\right)$(1) $a+4\times7=38$a+4×7=38 and find that $a$a is $10$10. The recurrence relation for this sequence is given by:

$T_n=T_{n-1}+7,T_1=10$Tn​=Tn−1​+7,T1​=10

Arithmetic sequences in tables and graphs

For any arithmetic sequence in the general form given by $T_n=a+\left(n-1\right)d$Tn​=a+(n−1)d, we can expand the bracket and collect like terms, creating a simplified generating rule of the form $T_n=dn+k$Tn​=dn+k where $d$d and $k$k are constants.

For example, the rule $T_n=5+\left(n-1\right)\times2$Tn​=5+(n−1)×2 is equivalent to $T_n=2n+3$Tn​=2n+3. This is in the form of the equation of a straight line $\left(y=mx+c\right)$(y=mx+c). If an arithmetic sequence is plotted as a series of points, they will all lie on a straight line with the gradient being the common difference. This makes sense since we have a constant rate of change in all arithmetic sequences.

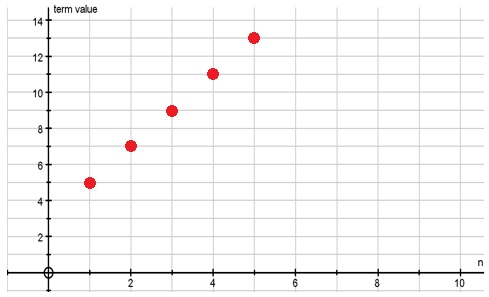
The first term is represented by the point shown at $n=1$n=1, $T_1=5$T1​=5 and we can see the gradient here is the common difference $d=2$d=2.

We could also be expected to recognise an arithmetic sequence from a table, such as:

$n$n	$1$1	$2$2	$3$3	$4$4	$5$5
$T_n$Tn​	$5$5	$7$7	$9$9	$11$11	$13$13

Here, we can read off the initial term $T_1=5$T1​=5 and the common difference can be seen in step between the $T_n$Tn​ values in the second row.

Use the following applet to explore the features of a graph that represents an arithmetic sequence.

Created with Geogebra

Applications of arithmetic sequences

Arithmetic sequences grow linearly, literally meaning ‘in a straight line’. We find applications of linear growth in many areas of life, including simple interest earnings, straight-line depreciation, monthly rental accumulation and many others. For example, if you are saving money in equal instalments the cumulative savings at each savings period form an arithmetic sequence. If you are travelling down a highway at a constant speed then the amount of petrol left in the tank, if measured every minute of the trip, forms another arithmetic progression. Whenever something grows or diminishes in constant quantities over equal time periods then that growth or decline is said to be linear.

Worked example

Example 3

Tabitha starts with $\$200$$200 in her piggy bank, the following week she adds $\$25$$25 and then continues to add $\$25$$25 at the start of each successive week. Find a rule to describe $B_n$Bn​ the balance of her savings at the start of the $n$nth week and find when her savings will reach $\$450$$450.

Think: The sequence of savings generated is $\$200,\$225,\$250,\$275...$$200,$225,$250,$275... This is arithmetic, so write down the starting value and common difference and use $T_n=a+\left(n-1\right)d$Tn​=a+(n−1)d to find a general rule.

Do: $a=200$a=200 and $d=25$d=25 and so our general rule is: $B_n=200+25(n-1)$Bn​=200+25(n−1) or equivalently $B_n=175+25n$Bn​=175+25n.

To find when the savings reach $\$450$$450, we substitute this into our general rule and solve for $n$n:

$450$450	$=$=	$175+25n$175+25n
$\therefore25n$∴25n	$=$=	$275$275
$n$n	$=$=	$11$11

Hence, at the start of the $11$11th week her savings will have grown to $\$450$$450.

Practice questions

Question 1

Question 2

Question 3

Question 4