Solving equations graphically
Consider the linear equation $2x+4=-6$2x+4=−6. We can immediately start solving it as shown below:
| $2x+4$2x+4 | $=$= | $-6$−6 |
| $2x+4-4$2x+4−4 | $=$= | $-6-4$−6−4 |
| $2x$2x | $=$= | $-10$−10 |
| $\frac{2x}{2}$2x2 | $=$= | $\frac{-10}{2}$−102 |
| $x$x | $=$= | $-5$−5 |
There is often more than one method available to us in mathematics. The graphical method is available for this question and we can solve $2x+4=-6$2x+4=−6 by treating each side of the equation as a separate function. We then sketch each function and see where they meet. Hence, we sketch the lines $y=2x+4$y=2x+4 and $y=-6$y=−6 and find the $x$x-coordinate of the point of intersection on the $xy$xy-plane.
We can see below that they intersect at the point $\left(-5,-6\right)$(−5,−6). This is consistent with the $x=-5$x=−5 we got when solving algebraically. (Remember, the $y$y value isn't important, as our original question was only in terms of $x$x.)

In general, if we have a linear equation like $ax+b=cx+d$ax+b=cx+d, then we can check the solution by sketching graphs of $y=ax+b$y=ax+b and $y=cx+d$y=cx+d.
There will usually be one solution, but none if the lines are parallel or an infinite number if the lines are collinear.
Solving linear inequalities graphically
Similar to linear equations, we can also make a connection between linear inequalities and graphs of lines. The key difference is that instead of just looking for where they intersect, we are interested in finding what range of $x$x-values one line is above or below the other.
Let's consider the inequality $3x-5>-5x+11$3x−5>−5x+11. On first reading, we can see we are finding $x$x values that make the left-hand side larger than the right-hand side. Graphically, this means we are seeking the values of $x$x for which the line $y=3x-5$y=3x−5 is greater than, or above, $y=-5x+11$y=−5x+11.
We can sketch graphs of both lines like this:
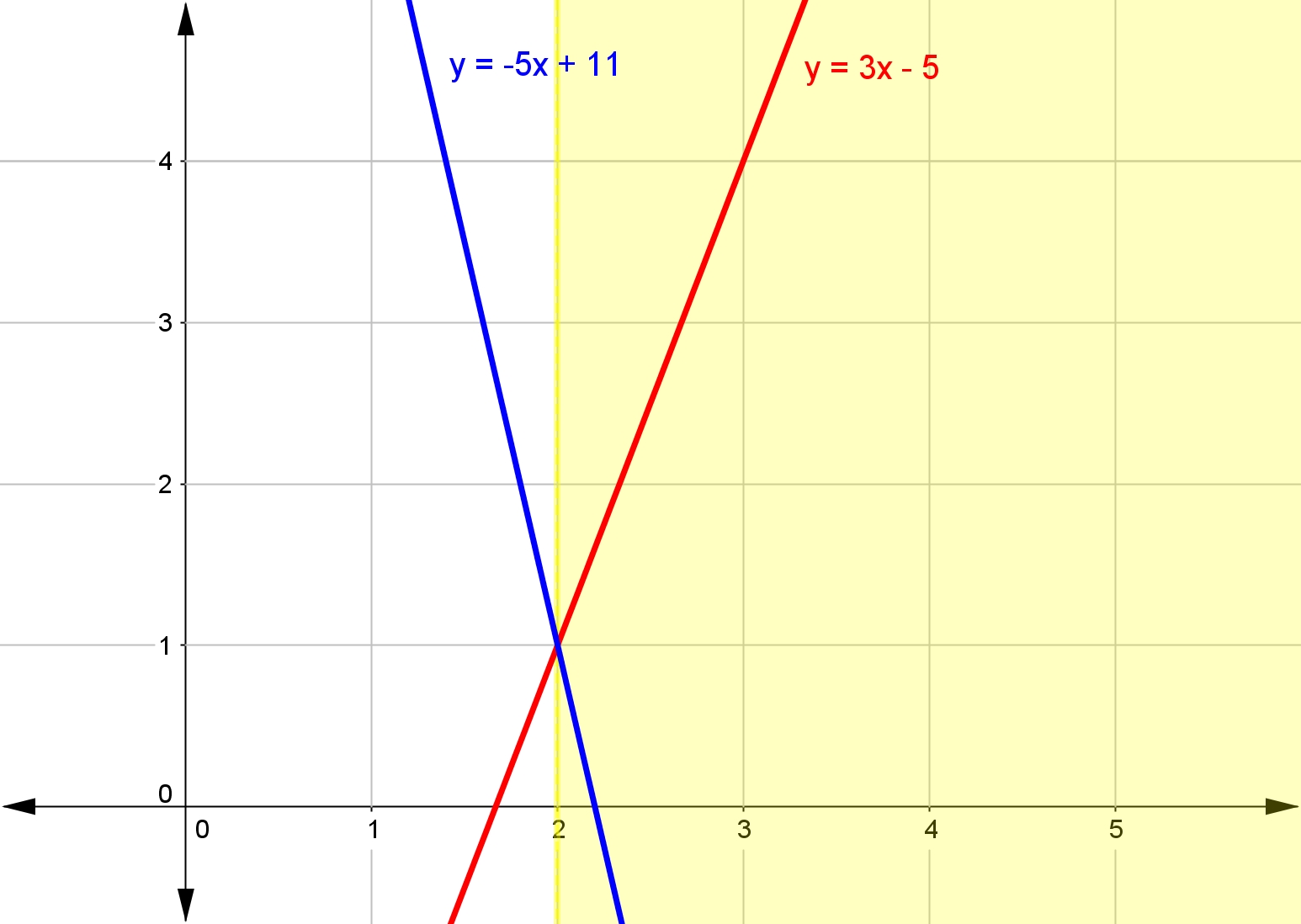
When is the line $y=3x-5$y=3x−5 above the line $y=-5x+11$y=−5x+11? It is clear that this occurs for $x>2$x>2.
Of course, we also have our algebraic skills to solve these questions, which means we are able to check our solution.
| $3x-5$3x−5 | $>$> | $-5x+11$−5x+11 | |
| $8x-5$8x−5 | $>$> | $11$11 | Add $5x$5x to both sides |
| $8x$8x | $>$> | $16$16 | Add $5$5 to both sides |
| $x$x | $>$> | $2$2 | Divide both sides by $8$8. |
Practice questions
Question 1
Consider the graphs of $y=x+5$y=x+5 and $y=12-x$y=12−x.
Using the graphs, state the solution of the inequality $x+5>12-x$x+5>12−x. Give your answer in interval notation.
Question 2
Consider the graphs of $y=x+6$y=x+6 and $y=x-7$y=x−7.
Which of the following statements is true?
The inequality $x+6\ge x-7$x+6≥x−7 has one solution.
AThe inequality $x+6\ge x-7$x+6≥x−7 has an infinite number of solutions.
BThe inequality $x+6\ge x-7$x+6≥x−7 has no solutions.
C
Equivalent inequalities
Suppose we want to solve $7-2x>-4x-12$7−2x>−4x−12. One approach would be to go through the slightly complicated task of sketching graphs of the line on the left and the line on the right to examine when the first lies above the second line. These graphs would have to be quite accurate to ensure we can clearly identify the points of intersection.
However, we could simplify the inequality first, bringing all of the terms to the left-hand side so that we only need to sketch one graph. Expanding and simplifying, we get:
| $7-2x$7−2x | $>$> | $-4x-12$−4x−12 |
| $7-2x+4x+12$7−2x+4x+12 | $>$> | $0$0 |
| $2x+19$2x+19 | $>$> | $0$0 |
The inequality $7-2x>-4x-12$7−2x>−4x−12 is thus equivalent to the inequality $2x+19>0$2x+19>0 from before, and so it will have the same solutions.
Practice question
Question 3
To solve the inequality $x\le\frac{x-3}{4}-1$x≤x−34−1, Tracy graphed $y=x-3$y=x−3. What other line would she need to graph to be able to solve the inequality graphically?
$y=4x+1$y=4x+1
A$y=\frac{x-3}{4}-1$y=x−34−1
B$y=x$y=x
C$y=4x+4$y=4x+4
D