8.05 Bearings

In surveying and navigation, bearings are used to help identify the location of an object.

The four main directions of a compass are known as cardinal directions. They are north (N), east (E), south (S) and west (W).

Three-figure (true) bearings

A three-figure bearing is:

• measured from north ($N$N)
• measured in a clockwise direction
• written using three figures

$T$T is often but not always used to indicate a three-figure bearing. If the angle measure is less than $100^\circ$100° it would be written like $040^\circ$040° or $040^\circ T$040°T.

To use true bearings to describe the location of a plane at point $B$B from the airport at point $A$A :

1. place the centre of a compass on the starting point, in this case the airport.
2. starting at North, rotate clockwise until we get to the line $AB$AB.
3. write the angle as the true bearing of point $B$B.

 

The bearing of $B$B from $A$A is $127^\circ$127° or $127^\circ$127°$T$T.

The diagram below describes the bearing of $P$P from $O$O. Rotating clockwise from North, we get an angle of $55^\circ$55°.

Since this measure is less than three digits, we put a 0 in front of it so the true bearing of $P$P is $055^\circ$055°.

Consider the bearing of $O$O from $P$P . Since alternate angles are equal and we are starting at $P$P the true bearing would be $180^\circ+55^\circ=235^\circ$180°+55°=235°.

 

Compass bearings

A compass bearing describes the location of a point using:

• the starting direction of either north or south;
• the acute angle needed to rotate
• the direction to rotate, east or west.

To describe the position of point $B$B from $A$A we would say:

"Starting at South, I then rotate $53^\circ$53° towards East."

 

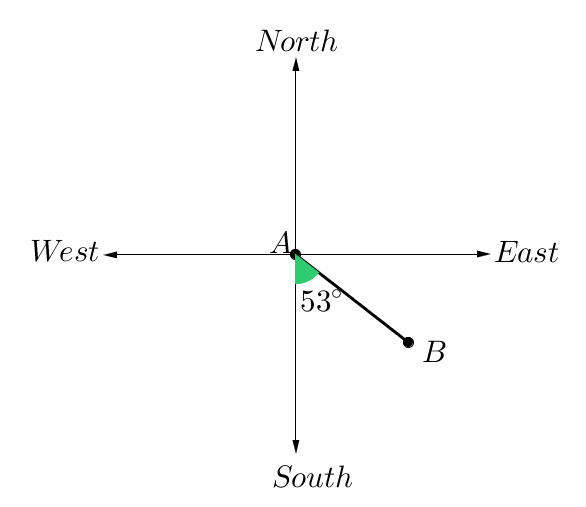
We can write this mathematically as $S\ 53^\circ E$S 53°E

Worked example

Example 1

Find the three-figure and compass bearings of point $P$P from $O$O.

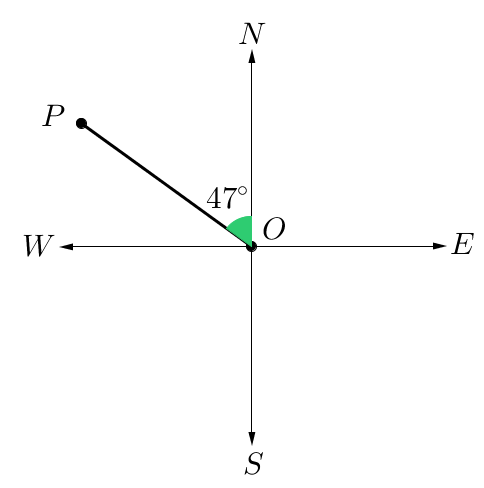
Three-figure bearing:

Starting at North rotate in a clockwise direction.

$360^\circ-47^\circ=313^\circ$360°−47°=313°

The three-figure bearing of $P$P from $O$O is $313^\circ T$313°T.

Compass Bearing

Point $P$P is closest to North, so starting at North, rotate $47^\circ$47° towards West.

The compass bearing of $P$P from $O$O is $N\ 47^\circ W$N 47°W.

 

Which one first?

The bearing needed or used completely depends on which position comes first. Have a look at the applet below, it quickly shows you how the angle changes depending on if we are measuring the bearing of A from B or B from A.

Created with Geogebra

 

Practice questions

Question 1

Question 2

Question 3

Applications

Worked example

Example 2

A slightly lost hiker walks $300$300 m east before turning south walking another $800$800 m. What is the hikers three-figure and compass bearings from the original position (rounded to one decimal place)?

Think: It will be easiest to first visualise the situation by drawing a diagram, such as this one:

For the three-figure bearing, the angle we want to find has been marked. It is equal to $90^\circ$90°$+$+the angle inside the triangle, which we can find using trigonometry. We can then use this to find the compass bearing.

Do: The three-figure bearing is

$90+\tan^{-1}\frac{800}{300}$90+tan−1800300​	$=$=	$90+\tan^{-1}\frac{8}{3}$90+tan−183​
	$=$=	$90+69.44395\ldots$90+69.44395…
	$=$=	$159.4$159.4 (one d.p.)

So the three-figure bearing is $159.4$159.4$^\circ$°.

To determine this as a compass bearing, we want to know the acute angle made with the North-South line. This is $180^\circ-159.4^\circ=20.6^\circ$180°−159.4°=20.6°.

Looking back at the diagram, we can see that this bearing is closer to South, and on the East side, so the compass bearing is $S\ 20.6^\circ E$S 20.6°E.

Practice questions

Question 4

Question 5