Trigonometric ratios in right-angled triangles
Pythagoras' theorem specifies a link between the sides of a right-angled triangle.
Pythagoras' theorem states for any right-angled triangle:

$a^2+b^2=c^2$a2+b2=c2
where $c$c represents the length of the triangle's hypotenuse and $a$a and $b$b are the lengths of the two other sides.
Special relationships also exist between the angles of right-angled triangles and the ratios of the length of sides.
When using these relationships we name the sides according to their position relative to a selected angle. If we have an angle indicated (like $\theta$θ in the diagram below) then we can label the three sides as follows:
Hypotenuse - is the name given to the longest side (always opposite the right angle).
Opposite Side - is the name given to the side opposite the angle in question.
Adjacent Side - is the name given to the side adjacent (next to) the angle in question.

Note the sides hypotenuse, opposite and adjacent are abbreviated to H, O and A.
For similar right-angled triangles (triangles with the same internal angles) the ratios of the sides will be equal. Consider the two similar triangles below, one twice the size of the other.

For both triangles the ratios of the sides are the same. For example, if we consider the $30^\circ$30° angle
| $\frac{O}{H}$OH | $=$= | $\frac{1}{2}$12 |
| $\frac{A}{H}$AH | $=$= | $\frac{\sqrt{3}}{2}$√32 |
| $\frac{O}{A}$OA | $=$= | $\frac{1}{\sqrt{3}}$1√3 |
If we consider an angle $\theta$θ in a right-angled triangle, we can construct ratios of the sides relative to position of this angle. These are called trigonometric ratios.
There are 3 basic trigonometric ratios. They have the special names of sine, cosine and tangent. We often shorten the names sine, cosine and tangent to sin, cos and tan respectively.

Right-angled triangle
$\sin\theta$sinθ = $\frac{Opposite}{Hypotenuse}$OppositeHypotenuse = $\frac{b}{c}$bc
$\cos\theta$cosθ = $\frac{Adjacent}{Hypotenuse}$AdjacentHypotenuse = $\frac{a}{c}$ac
$\tan\theta$tanθ = $\frac{Opposite}{Adjacent}$OppositeAdjacent = $\frac{b}{a}$ba
The mnemonic SOHCAHTOA can be useful to help remember the ratios.
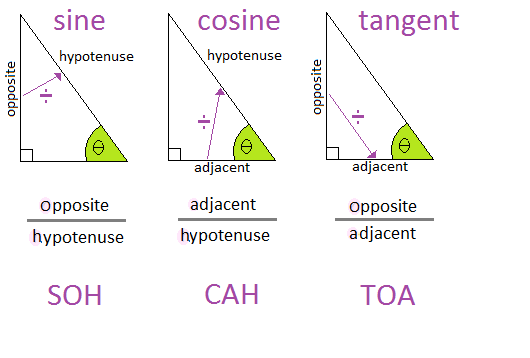
These three trigonometric ratios allow us to find unknown sides and lengths of right-angled triangles.
Worked examples
Example 1

In the triangle shown $\theta=25^\circ$θ=25° and the length of the hypotenuse is 12.6. Find $b$b.
Think: We need to identify the sides we have and want with respect to the angle given. Here I can see that we have the hypotenuse (H) and we want b, which is opposite (O) the angle. This means I have OH - so the trig ratio I need to use here is sine.
Do:
| $\sin\theta$sinθ | $=$= | $\frac{O}{H}$OH |
| $\sin25^\circ$sin25° | $=$= | $\frac{b}{12.6}$b12.6 |
| $b$b | $=$= | $12.6\times\sin25^\circ$12.6×sin25° |
| $b$b | $=$= | $5.32$5.32 |
example 2
Find the length of the hypotenuse when $\theta=36^\circ$θ=36° and the given side length of 4.8

Think: We need to identify the sides we have and want with respect to the angle given. Here I can see that we want the hypotenuse (H) and we have a side length of 4.8, which is adjacent (A) the angle. This means I have AH - so the trig ratio I need to use here is cosine.
Do:
| $\cos\theta$cosθ | $=$= | $\frac{A}{H}$AH |
| $\cos35^\circ$cos35° | $=$= | $\frac{4.8}{c}$4.8c |
| $c$c | $=$= | $4.8\times\cos35^\circ$4.8×cos35° |
| $c$c | $=$= | $3.93$3.93 |
Example 3
Find the value of the angle indicated given the side lengths shown. 
Think: We need to identify the sides we have with respect to the angle we want to find. Here I can see that we have the opposite (O) and adjacent (A) sides. This means I have OA - so the trig ratio I need to use here is tangent.
Do:
Use the inverse operation to find an angle given a ratio.
| $\tan\theta$tanθ | $=$= | $\frac{O}{A}$OA |
| $\tan\theta$tanθ | $=$= | $\frac{14.77}{12.24}$14.7712.24 |
| $\theta$θ | $=$= | $\tan^{-1}\left(\frac{14.77}{12.24}\right)$tan−1(14.7712.24) Use the inverse operation (shift + tan on your calculator) to find an angle given a ratio. |
| $\theta$θ | $=$= | $50.35^\circ$50.35° |
Practice Questions
Question 1
Find the value of $f$f, correct to two decimal places.

An inverted right triangle with its base on top. The angle on the left vertex of the base is $47^\circ$47°. Adjacent to this angle is the base of the triangle labeled as "$f$f m," indicating its unknown length. The angle on the right vertex of the base is a right angle as indicated by a small square. Opposite the right angle is the hypotenuse labeled "$8$8 m," indicating its length.
Question 2
Find the value of $h$h, correct to two decimal places.

Question 3
Find the value of $x$x to the nearest degree.

A right-angled triangle with vertices labeled A, B and C. Vertex A is at the top, B at the bottom right, and C at the bottom left. A small square at vertex A indicates that it is a right angle. Side interval(BC), which is the side opposite vertex A, is the hypotenuse and is marked with a length of 25. The angle located at vertex B is labelled x. Side interval(AB), descending from the right angle at vertex A to vertex B, is marked with a length of 7, and is adjacent to the angle x. Side interval(AC) is opposite the angle x.
Question 4
Consider the following triangle.

A right-angled triangle with vertices labeled $A$A, $B$B, and $C$C. Each of the non-right angles at vertices $A$A and $B$B is marked with a small arc near the vertex. Vertex $C$C has a right angle, indicated by a small square corner. An angle $\theta$θ is indicated at vertex $B$B. Side $BC$BC is labelled 5 and is adjacent the angle theta. Side $AC$AC is labelled 12 and is opposite the angle $\theta$θ. Side $AB$AB is the hypotenuse and labelled x.
Find the value of $x$x.
Hence find the value of $\sin\theta$sinθ. Express your answer as a simplified fraction.
Hence find the value of $\cos\theta$cosθ. Express your answer as a simplified fraction.
Working with degrees, minutes and seconds
We've already looked at how to find angles using trigonometric ratios and we are used to giving our answers as whole numbers or decimals. Now we are going to look at another way to express a part of a degree using minutes and seconds.
There are $60$60 minutes in $1$1 degree.
There are $60$60 seconds in $1$1 minute.
Converting decimals to minutes and seconds
To convert a number in decimal form into minutes and seconds, we need first to find what number out of $60$60 the decimal part of the number represents.
For example, let's say we wanted to round $15.72^\circ$15.72° to the nearest minute.
We need to work out $15^\circ$15° + $0.72$0.72 of a degree, which is $15^\circ$15° plus $0.72$0.72 of $60$60 minutes.
| $0.72\times60$0.72×60 | $=$= | $43.2$43.2 minutes |
So, $15.72^\circ$15.72° rounded to the nearest minute is $15^\circ$15°$43$43'.

Converting on a calculator
There are also some buttons our your calculator to help you work with minutes and seconds.
The button highlighted in blue allows you to write degrees and minutes in your calculator. Push the button after you've entered the number of degrees, then again after minutes, and again after seconds if you have them. After you've found an answer, pushing this button will toggle between the decimal and degrees/minutes/seconds form.
The button highlighted in green will convert between decimals and fractions.
Rounding
Rounding minutes and seconds is similar to rounding decimals. However, because there are $60$60 minutes in a degree and $60$60 seconds in a minute, our half way point is $30$30.
- If the minutes are below $30$30, we round down to the nearest degree.
- If the minutes are $30$30 or above, we round up to the nearest degree.
- If the seconds are below $30$30, we round down to the nearest minute.
- If the seconds are $30$30 or above, we round up to the nearest minute.
Practice questions
Question 5
Convert the following into degrees and minutes:
$24.4^\circ$24.4°=$\editable{}$ degrees $\editable{}$ minutes
Question 6
Round $25^\circ$25°$49$49'$40$40" to the nearest minute.
$\editable{}$° $\editable{}$'
Question 7
Consider the following diagram.

Find the value of $x$x correct to 2 decimal places.
Hence find $x$x to the nearest minute.