When we learnt about box plots we saw that data can come in all different shapes and sizes. Sometimes there are lots of low scores, sometimes there are lots of high scores and sometimes most of the scores are right in the middle.
When we describe the shape of data sets, we want to focus on how the scores are distributed and whether the shape is symmetrical or not.
Symmetry
Data may be described as symmetrical or asymmetrical.
There are many cases where the data tends to be around a central value with no bias left or right. In such a case, roughly $50%$50% of scores will be above the mean and $50%$50% of scores will be below the mean.
The normal distribution is the most common example of symmetrical data. The normal distribution looks like this:
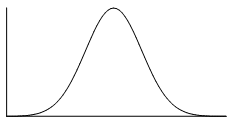
The picture below shows how the normal distribution can occur on a histogram. The dark line shows the nice, symmetrical polygon that can be drawn over the histogram.
In the distribution below, the $0$0 point in the middle represents the mean, the median and the mode - all these measures of central tendency are equal for this distribution, since it is symmetrical. If we use the line at $0$0 as our axis of symmetry, notice that the left hand side is a perfect reflection of the right hand side.

Skew
If a data set is asymmetrical instead (i.e. it isn't symmetrical), it may be described as skewed.
Positive skew
A data set that has positive skew (sometimes called a 'right skew') has a long tail of values above the peak of the graph, such that more than half of the scores are above the peak. This means the mean is greater than the median, which is greater than the mode.
MODE < MEDIAN < MEAN
A positively skewed graph looks something like this.
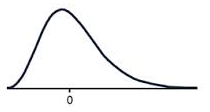
Notice that there are more scores above the peak than below the peak?
Negative skew
A data set that has negative skew (sometimes called a 'left skew') has a long tail of values below the peak of the graph, such that more than half of the scores are below the peak. This means the mode is greater than the median, which is greater than the mean.
MEAN < MEDIAN < MODE
A negatively skewed graph looks something like this.
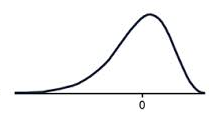
Notice that there are more scores below the peak than above the peak?
Clustering
In a set of data, a cluster occurs when a large number of the scores are grouped together within a very small range.
Outliers
The shape of a data also shows us whether there are any outliers or unusually high or low scores in our data set.
For example, in the dot plot below, do you see how all the scores range between $12$12 and $14$14 except one? This means that $24$24 is an outlier.

In this case the data is very obviously way outside the range of the rest of the data set.
We have seen in a previous chapter that we can more formally define an outlier as a score that is more than $1.5\times$1.5×IQR above the upper quartile, or more than $1.5\times$1.5×IQR below the lower quartile.
Practice questions
Question 1
State whether the scores in each histogram are positively skewed, negatively skewed or symmetrical (approximately).
A histogram that represents the distribution of scores. The x-axis enumerates discrete scores as individual points, while the y-axis corresponds to the frequency of each score interval. Each bar on the histogram corresponds to one of these distinct scores, with the bar's height reflecting the count or frequency of occurrences for that particular score. Most of the scores are relatively high. Positively skewed
ASymmetrical
BNegatively skewed
CA histogram that represents the distribution of scores. The x-axis enumerates discrete scores as individual points, while the y-axis corresponds to the frequency of each score interval. Each bar on the histogram corresponds to one of these distinct scores, with the bar's height reflecting the count or frequency of occurrences for that particular score. Approximately, as the score goes higher, the frequency goes lower. Positively skewed
ANegatively skewed
BSymmetrical
CA histogram that represents the distribution of scores. The x-axis enumerates discrete scores as individual points, while the y-axis corresponds to the frequency of each score interval. Each bar on the histogram corresponds to one of these distinct scores, with the bar's height reflecting the count or frequency of occurrences for that particular score. The scores have its peak approximately in the middle. Negatively skewed
ASymmetrical
BPositively skewed
C
QUESTION 2
The table shows the number of crime novels in a bookshop for different price ranges.
| Price of crime novel to nearest $\$5$$5 | Frequency |
|---|---|
| $5$5 | $5$5 |
| $10$10 | $10$10 |
| $15$15 | $17$17 |
| $20$20 | $8$8 |
| $25$25 | $17$17 |
| $30$30 | $10$10 |
| $35$35 | $5$5 |
Plot this data as a histogram.
Which of the following best describes the data in the graph and table?
Symmetrical
ARight skewed
BLeft skewed
CUniform distribution
D
QUESTION 3
For the Stem and Leaf plot attached:
| Stem | Leaf | |
| $0$0 | $5$5 | |
| $1$1 | $7$7 $8$8 | |
| $2$2 | $0$0 $8$8 | |
| $3$3 | $0$0 $4$4 $6$6 $7$7 $8$8 $9$9 | |
| $4$4 | $1$1 $3$3 $5$5 $8$8 $8$8 $8$8 | |
| $5$5 | ||
| $6$6 | ||
| $7$7 | ||
| $8$8 | ||
| $9$9 | $3$3 | |
|
||
Are there any outliers?
Yes
ANo
BIdentify the outlier.
Is there any clustering of data?
Yes
ANo
BWhere does the clustering occur?
10s - 20s
A30s - 40s
B20s - 30s
CWhat is the modal class(es)?
10-19
A40-49
B30-39
C20-29
DNot including the outlier, the distribution of the data is:
Positively skewed
ASymmetrical
BNegatively skewed
C
Central tendency
So far we have learnt about three measures of central tendency: the mean, the median and the mode. These three measures all give us an approximation of where the centre is in a data set.
So when we are able to recognise the centre of data sets by finding the mean, median and mode, we can start to compare and make judgments about different data sets. We can say which one has the highest mode, the lowest median and so on.
Modality
Modality describes the prevalence of local peaks in a data set. The peaks don't necessarily need to be the mode of the whole data set, but rather a local cluster of data that is more frequent and stands out from the surrounding data. When we look at the modality of a data set, it is usually useful to examine a graph of the data.
We describe modality by the number of peaks. A data set that has two distinct peaks, like in the frequency polygon below, is called bimodal.

To determine the modality of a distribution, we can simply identify the number of modal peaks. For instance, we would say that the data shown in the dot plot below has three modal peaks because there are local peaks at scores of $6$6, $12$12, and $20$20.
Practice questions
Question 4
For each of the following statements, decide whether they are true or false:
If two sets of data have the same median then the data sets must themselves be the same
True
AFalse
BIf two sets of data have very different modes then the highest values cannot be the same
True
AFalse
B
QUESTION 5
From the frequency polygon shown:
Find the number of scores.
Calculate the sum of the scores.
Calculate the mean of the scores, correct to 2 decimal places.
QUESTION 6
How many peaks are there on the graph?

$\editable{}$ peaks
Choosing a measure of centre
While we have learned about three measures of central tendency (the mean, median and mode), it is important to note that certain features in a data set can significantly affect one or more of these measures of central tendency.
So how do we know which measure of central tendency is most appropriate for a data set?
Mode
Remember the mode is the most frequently occurring score. So if we notice that a data set has a significant number of repeated scores, then the mode could be a good measure of centre.
Mean
If the range of scores is reasonably small and there are no outliers, then the mean is an appropriate measure of centre.
Median
Unlike the mean, the median is not affected by outliers. So the median is a good measure of central tendency if a data set has outliers or a large range.
Choosing a measure of centre from a graph
The shape of the data may also determine which measure of central tendency is the most appropriate measure of a data set.
If a data set is symmetrical, then the mean and median will be approximately equal. If the data is unimodal (has only one mode) then the mode will also be approximately equal. If the data has more than one mode (e.g. if it is bimodal) then the modes may be different to the mean and median.
When data is positively skewed, the mean is usually the highest measure of central tendency and the mode is usually the lowest measure of central tendency.
For positively skewed data:
MODE < MEDIAN < MEAN
When data is negatively skewed, the mode is usually the highest measure of central tendency and the mean is usually the lowest measure of central tendency.
For negatively skewed data:
MEAN < MEDIAN < MODE
Therefore, in skewed data, the most appropriate measure of central tendency will be the median.
Summary
Here is a basic summary of selecting an appropriate measure of central tendency. Note that often it can be helpful to consider more than one measure.
| Data Set... | Mean | Median | Mode |
|---|---|---|---|
| has outliers | |||
| has many repeated values | |||
| has a relatively small range | |||
| is skewed |
But of course, sometimes the context of the data we are analysing lends itself to particular measures as well.
Practice questions
Question 7
Which measure of centre would be best for the following data set?
$15,13,16,17,15,15,15$15,13,16,17,15,15,15
Mean
AMode
BMedian
C
QUESTION 8
Which measure of centre would be best for the following data set?
$8,10,14,18,19,91$8,10,14,18,19,91
Mean
AMedian
BMode
C
QUESTION 9
Every week over $45$45 weeks, a kayaking club runs social sessions that are open to the public. On each session, the number of people who attend is recorded. The results are displayed in the table provided.
| Number of people attending | Number of Weeks |
|---|---|
| $12$12 | $6$6 |
| $13$13 | $5$5 |
| $14$14 | $6$6 |
| $15$15 | $5$5 |
| $16$16 | $6$6 |
| $17$17 | $5$5 |
| $18$18 | $6$6 |
| $19$19 | $5$5 |
| $20$20 | $6$6 |
Considering the distribution of the responses, which of the following is true?
The mean is a better indicator of the typical number of people who attended each session than the median.
AThe median is a better indicator of the typical number of people who attended each session than the mean.
BThe mean and median are equally accurate indicators of the typical number of people who attended each session.
C
QUESTION 10
What measure of center would be most appropriate to use to represent the data in this graph?
Median
AMode
BMean
C

