Surface area of composite solids
We know that surface area is the total area of all the faces on a 3D object. We have looked at surface area of prisms, pyramids, cylinders and spheres.
Sometimes though, the shape is a composite solid, which means it is made up of a combination of solids. The following diagrams are all examples of composite solids:
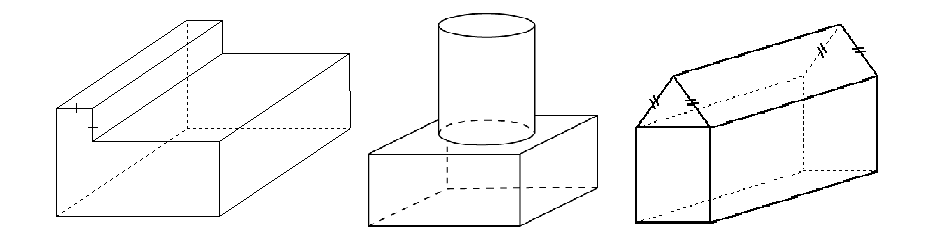
To find the surface area of these solids, we need to visualise the different shapes that make up the visible surfaces. Generally, there are less surfaces in total compared with the separate solids, because they have been formed by joining two faces together. For example, in the middle diagram above, we would need to calculate the area of the base circle of the cylinder and subtract it from the top surface of the rectangular prism, as the solid is considered to be joined there.
Once we have identified the different faces, we can calculate the areas and add them up.
A common mistake is to forget faces that we may not be able to see in the diagram, like those at the back or bottom of the shape that is given.
Worked example
Find the surface area of the following solid shape:

Working step by step and identifying each face and its duplicates is a good way to approach these problems. Let's get started.
Start with the easier rectangular faces of the prism and cylindrical faces as follows:

| Area of two end faces | $=$= | $2\times10\times12$2×10×12 | $=$=$240$240m2 |
| Area of two side faces | $=$= | $2\times10\times21$2×10×21 | $=$=$420$420m2 |
| Area of bottom face | $=$= | $12\times21$12×21 | $=$=$252$252m2 |
| Area of top of cylinder | $=$= | $\pi\times4^2$π×42 | $=$=$50.3$50.3m2 |
| Area of cylinder curved face | $=$= | $2\pi\times4\times7$2π×4×7 | $=$=$175.9$175.9m2 |
There is only one face left to deal with and it can be useful to visualise looking from above, or taking a birds eye or plan view of the solid as follows:

From this view we can see the surface is a rectangle, the same as the base with the base of the cylinder removed. As we have already calculated these areas we can use them to find the area of this surface as follows:
| Area of composite surface | $=$= | $252-50.3$252−50.3 | $=$=$201.7$201.7m2 |
Therefore total surface area is the addition of all the calculated areas:
| Total surface area of solid | $=$= | $240+420+252+50.3+175.9+201.7$240+420+252+50.3+175.9+201.7 | $=$=$1339.9$1339.9m2 |
Practice questions
Question 1
In the diagram, the roof has a height of $3$3 metres. Find the surface area of the figure shown,
Round your answer to two decimal places.

Question 2
Find the surface area of the figure shown.
