Subtracting vectors combines the ideas of negative vectors and addition.
Remember how a negative vector has same size but opposite direction, well this means that the concept of subtracting a vector is the same as adding its negative.
That is that
$a-b=a+(-b)$a−b=a+(−b)
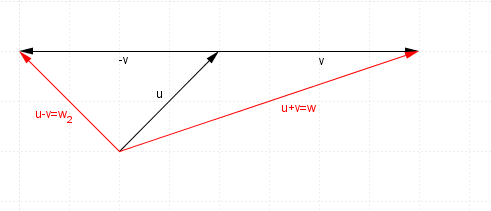
Geometrically it looks like this
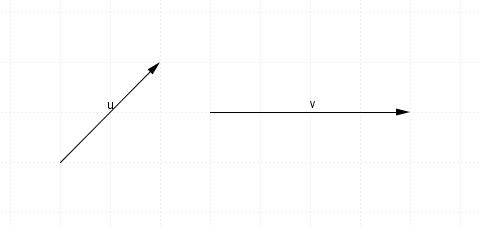
here are vectors $u$u and $v$v
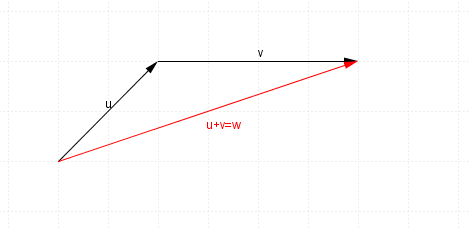
$u+v$u+v will look like this (remember to head to tail it)
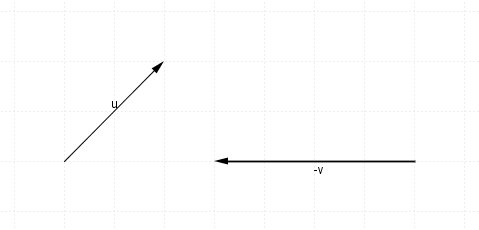
$-v$−v will look like this, (same size as $v$v, just opposite direction)
and hence $u-v$u−v, or $u+-v$u+−v will look like this
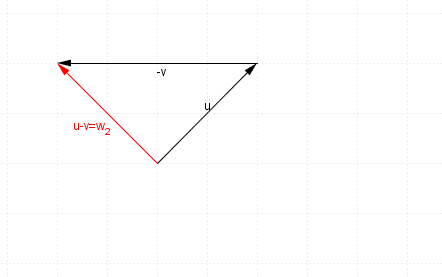
Here are both situations to compare on the one diagram
Of course if we use matrix notation, then this becomes a simple process of matrix subtraction.
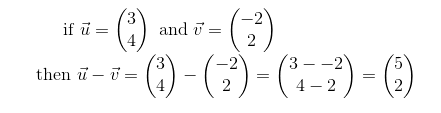
This applet will allow you to practice making vectors, and then demonstrate their subtraction via a geometric representation.