Areas of Triangles, Quadrilaterals and Composite Shapes

Areas of Rectangles

A rectangle is a shape with the specific geometric properties of 

• opposite sides equal in length
• opposite sides parallel
• sides meet at right angles.

To determine the area of a rectangle we divide the rectangle up into square units and count them up.

Here is a rectangle measuring $4$4 units in length and $2$2 units in width. 

	We divide the rectangle up into its square units and see how many there are
	This rectangle has an area of 8 square units.

 

How did we get 8?  Well, we could count the squares $1$1 at a time.  Or we could use multiplication by seeing that there are $2$2 rows of $4$4, ($2\times4=8$2×4=8) or that there are $4$4 columns of $2$2 ($4\times2=8$4×2=8).  Did you notice? These were the lengths of the sides.  

This is great, it looks like we have found a simple way of finding the area of rectangles.  We turn the rectangle into an array based on the lengths of the sides and multiply. 

See these:

	$1\times4$1×4	rectangle has area of	$1\times4=4$1×4=4 square units
	$2\times3$2×3	rectangle has area of	$2\times3=6$2×3=6 square units
	$6\times3$6×3	rectangle has area of	$6\times3=18$6×3=18 square units

 

Of course we don't have to draw in all the little squares every time. Now that we understand the array structures within rectangles we can just use the rule to find the area of a rectangle.

 

Knowing the area of a rectangle is a very powerful thing!  As you will see in the next few chapters, areas of rectangles will help us find the areas of squares, triangles, parallelograms, trapezoids and even more!

Area of Squares

A square is a shape with the specific geometric properties of 

• opposite sides equal in length
• opposite sides parallel
• sides meet at right angles

AND

• all sides equal.

This makes a square a very special kind of rectangle, because it meets all the requirements of a rectangle but has one extra special geometric property.  

To find the area of a square, we use the rectangle rule,  

$A=L\times W$A=L×W

but because the $L$L and $W$W are the same, then the area of a square is just 

 

See these squares

		Area	$=$=	$3\times3$3×3
			$=$=	$9$9 square units
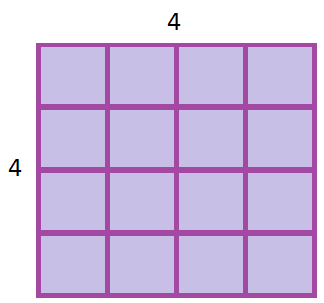		Area	$=$=	$4\times4$4×4
			$=$=	$16$16 square units

 

Units

We use special units to describe area, based on the notion of square units described above.  Because the units for length include millimetres, centimetres, metres and kilometres we end up with the following units for area.

TRIANGLES

Did you know a rectangle can be drawn around every single triangle. See these:

 

But what is really amazing about these constructions is that the area of the triangle is exactly equal to the area of the extra triangles we added to make the rectangles!

Check out the mathlet below to see for yourself.  Drag the vertices of the triangle to change its shape and then slide the slider to see how it turns into a rectangle.

Why does this matter?

Well we already know how to find the area of a rectangle ($A=L\times W$A=L×W), and the interactive above shows us that the triangle is half of that!

This means that the 

 

​

Parallelogram

A parallelogram is a shape with the specific geometric properties of 

• opposite sides equal in length
• opposite sides parallel

Let's take a look at an interesting property of parallelograms.

​

From the interactive above can you see how easily a parallelogram turns into a rectangle?   

And guess what.  Because we know the $\text{Area of a rectangle }=L\times W$Area of a rectangle =L×W, then we can work out the area of any parallelogram.

We tend to call the bottom side of the parallelogram a BASE, and we also need the HEIGHT of the parallelogram.  (remember it is exactly the same as the area of a rectangle even if the rule uses different words to length and width)

Thus we get that the

Example

Let's do an example using our new rule,

Find: The area of this parallelogram

Think: Identify the values for the base and height

Do:

A	$=$=	$b\times h$b×h
	$=$=	$32\times14$32×14 mm2
	$=$=	$30\times14+2\times14$30×14+2×14 mm2
	$=$=	$420+28$420+28 mm2
	$=$=	$48$48 mm2

 

Trapezoid

A trapezoid (sometimes called trapezoid) is a 2D shape with the specific geometric properties of 

• 1 pair of opposite sides that are parallel

All of these are trapezoids

 

Area of a trapezoid

Let me show you something.

Move the point D anywhere you like to create a trapezoid and then slide the green slider to the right.

​

From the interactive you can see you to flip the trapezoid over and turn it into a parallelogram, and of course we already know that a parallelogram has the same area as a rectangle!

And guess what.  Because we know the $\text{Area of a rectangle }=L\times W$Area of a rectangle =L×W, then we can work out the area of any trapezoid.

We tend to call the top side of the trapezoid  BASE 1 (a), and we call the bottom side BASE 2 (b) - because when we flip it both those sides becomes part of the base. We also need the HEIGHT of the trapezoid.  

Thus we get that the

You might wonder why we divide this by two.  Well remember we flipped the trapezoid over to turn it into a rectangle, well that means that 2 trapezoids is the same as the parallelogram - but we really only want the area of 1 trapezoid.  

Lets do an example using our new rule

Example

Question: A new chocolate bar is to be made with the following dimensions,  the graphic artist needs to know the area of the trapezoid to begin working on a wrapping design.  Find the area.  

Think: I need to identify the base1, base2 and height.  I can see these on the diagram that is given.

Do:

$\text{Area of a Trapezoid}$Area of a Trapezoid	$=$=	$\frac{1}{2}\times\left(\text{Base 1 }+\text{Base 2}\right)\times\text{Height }$12​×(Base 1 +Base 2)×Height
	$=$=	$\frac{1}{2}\times\left(a+b\right)\times h$12​×(a+b)×h
	$=$=	$\frac{1}{2}\times\left(4+8\right)\times3$12​×(4+8)×3
	$=$=	$\frac{1}{2}\times12\times3$12​×12×3
	$=$=	$18$18 cm2

So now we can find the areas of rectangles, triangles (which are half of a rectangle), parallelograms (like a rectangle) and trapezoids (like half a rectangle).

Kite

A kite is a 2D shape with the specific geometric properties of 

• 2 pairs of adjacent sides that are equal
• 1 pair of equal angles

Of course the kite you fly around on a windy day is named after the geometric shape it looks like.

Kites can taken on many different shapes and sizes. Try moving points $A$A, $O$O and $D$D on this mathlet to make many kinds of kites.

 

Area of a Kite

Let me show you something. Slide the slider.  What shape is created?  Now try showing diagonals and then sliding the slider.  

 

​

From the interactive you'll notice that if you copy the inner triangles of the kite and rearrange them you can create - you guessed it a rectangle.  Of course, like the trapezoid, our original shape is only 1/2 of this rectangle. 

Because we know the $\text{Area of a rectangle }=L\times W$Area of a rectangle =L×W, then we can work out the area of any kite.

We tend to call the long diagonal $x$x and we call the short diagonal of the kite $y$y.   These give us the length and width of the rectangle that the kite fits inside. 

Let's do an example using our new rule.

Example

Question: Find the area of this kite  

Think: I need to identify the long diagonal length and the short diagonal length.

Do:

$\text{Area of a Kite }$Area of a Kite	$=$=	$\frac{1}{2}\times x\times y$12​×x×y
	$=$=	$\frac{1}{2}\times4\times\left(2\times0.9\right)$12​×4×(2×0.9)
	$=$=	$\frac{1}{2}\times4\times1.8$12​×4×1.8
	$=$=	$3.6$3.6 mm2

 

RHOMBUS

A rhombus is a 2D shape with the specific geometric properties of 

• all sides equal in length
• opposite sides parallel
• opposite angles equal
• diagonals bisect each other

You can play with this mathlet to make many kinds of rhombuses, it also shows that you only need 1 side length and 1 angle to create one.  

Area of a rhombus

Let me show you something;

​

From this interactive you can see that as you copy the inner triangles of the rhombus and place them accordingly you can create - you guessed it a rectangle.  Of course, like the trapezoid and kite, our original shape is only $\frac{1}{2}$12​ of this rectangle. 

Because we know the $\text{Area of a rectangle }=L\times W$Area of a rectangle =L×W, then we can work out the area of any rhombus.

Lets call the diagonals $x$x and $y$y.   These give us the length and width of the rectangle that the rhombus fits inside.

 

So now lets do an example using our new rule

Example

Question: A packing box with a square opening is squashed into the rhombus shown.  What is the area of the opening of the box?

Think: I need to be able to identify the two diagonals.

Do:

$\text{Area of a Rhombus }$Area of a Rhombus	$=$=	$\frac{1}{2}\times\text{diagonal 1 }\times\text{diagonal 2 }$12​×diagonal 1 ×diagonal 2
	$=$=	$\frac{1}{2}\times x\times y$12​×x×y
	$=$=	$\frac{1}{2}\times16\times4$12​×16×4
	$=$=	$32$32 cm2

 

 

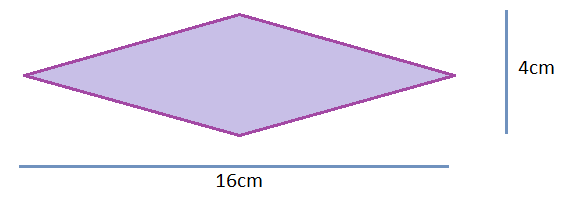
So now we can find the areas of rectangles, triangles (which are half of a rectangle), parallelograms (like a rectangle), trapezoids (like half a rectangle), kites (like half a rectangle) and now rhombuses (like half a rectangle).

We have already had a look at combining 2D shapes together and finding the area of composite shapes.  But since then we have learnt about the areas of a whole lot more shapes.  

Let's just look at a summary of areas of 2D shapes we have looked at so far with our shape robot:

Strategies

The key skills you need to remember when thinking about composite shapes are to consider

• can the shape be considered as a larger easier shape with smaller bits missing
• can the shape be considered the sum of a number of smaller shapes

$\text{Area of a Rectangle }=\text{length }\times\text{width }$Area of a Rectangle =length ×width

$A=L\times W$A=L×W

$\text{Area of a Square }=\text{Side }\times\text{Side }$Area of a Square =Side ×Side

$A=S\times S$A=S×S

$\text{area of a triangle }=\frac{1}{2}\times\text{base }\times\text{height }$area of a triangle =12​×base ×height

$A=\frac{1}{2}bh$A=12​bh

$\text{Area of a Parallelogram }=\text{Base }\times\text{Height }$Area of a Parallelogram =Base ×Height

$A=b\times h$A=b×h

$\text{Area of a Trapezoid}=\frac{1}{2}\times\left(\text{Base 1 }+\text{Base 2 }\right)\times\text{Height }$Area of a Trapezoid=12​×(Base 1 +Base 2 )×Height

$A=\frac{1}{2}\times\left(a+b\right)\times h$A=12​×(a+b)×h

$\text{Area of a Kite}=\frac{1}{2}\times\text{diagonal 1}\times\text{diagonal 2}$Area of a Kite=12​×diagonal 1×diagonal 2

$A=\frac{1}{2}\times x\times y$A=12​×x×y

$\text{Area of a Rhombus }=\frac{1}{2}\times\text{diagonal 1}\times\text{diagonal 2}$Area of a Rhombus =12​×diagonal 1×diagonal 2

$A=\frac{1}{2}\times x\times y$A=12​×x×y

$\text{Area of a circle }$Area of a circle

$A=\pi r^2$A=πr2

$\text{Area of a sector }$Area of a sector

$A=\frac{\text{angle of sector}}{360}\times\pi r^2$A=angle of sector360​×πr2