Reviewing some basic graph types
Let's first recall the basic graphs as shown here in the diagram. The function's description is given below each graph. For example the linear function $y=mx+b$y=mx+b is shown on the left and the hyperbola $y=\frac{1}{x}$y=1x is shown second from right.

Two of the graphs are shown with some generalising coefficients - the line $y=mx+b$y=mx+b and the exponential curve $y=a^x$y=ax. Thus we could site particular examples of these graphs such as $y=2x+5$y=2x+5, $y=7x$y=7x and $y=3^x$y=3x etc.
However, all of these basic types can be generalised further by what are known as transformations.
Translations
One common transformation is known as a translation. This is a horizontal and/or vertical shift in the position of the curve relative to the cartesian axes. Translations are easy to recognise.
If we replace $x$x with $\left(x-h\right)$(x−h), the basic curve is moved $h$h units to the right. If we replace $x$x with $\left(x+h\right)$(x+h), the basic curve is moved $h$h units to the left. If we replace $y$y with $\left(y-k\right)$(y−k), the basic curve is moved $k$k units up. If we replace $y$y with $\left(y+k\right)$(y+k), the basic curve is moved $k$k units down.
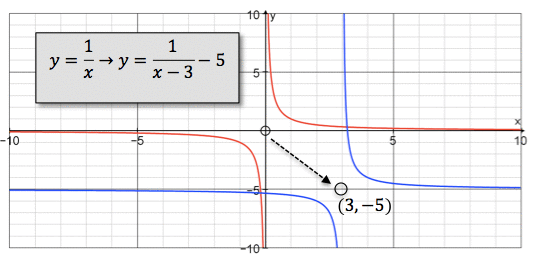
So suppose we take the hyperbola $y=\frac{1}{x}$y=1x and translate it $3$3 units to the right and $5$5 units down. The new function becomes $y+5=\frac{1}{x-3}$y+5=1x−3, or expressed explicitly $y=\frac{1}{x-3}-5$y=1x−3−5. The vertical and horizontal asymptotes are respectively $x=3$x=3 and $y=-5$y=−5.
If we take the parabola $y=x^2$y=x2 and shift it $1$1 unit to the left and $5$5 units up, the new function becomes $y-5=\left(x-1\right)^2$y−5=(x−1)2 . Again, we can express this explicitly as $y=\left(x-1\right)^2+5$y=(x−1)2+5.

If we take the function $y=x^3$y=x3 and translate it $2$2 units to the right and $1$1 unit up, the new function is given by $y-1=\left(x-2\right)^3$y−1=(x−2)3, expressible as $y=\left(x-2\right)^3+1$y=(x−2)3+1.

Dilations and reflections
Another type of transformation is commonly referred to as a dilation. This is when a curve is stretched or compressed by some factor other than $1$1 in the function's equation.
For example, the difference between $y=x^2$y=x2 to $y=3x^2$y=3x2 is the dilation factor $3$3. Every function value in $y=3x^2$y=3x2 is $3$3 times the associated function value in $y=x^2$y=x2. This means that the curve becomes steeper.
Again, every function value of the function $y=\frac{2}{x}$y=2x is double the associated function value of $y=\frac{1}{x}$y=1x.
Every function value of $y=3\left(2^x\right)$y=3(2x) is $3$3 times that of $y=2^x$y=2x, and every function value of $y=\frac{1}{2}x^3$y=12x3 is one-halve that of $y=x^3$y=x3.
We can also reflect a curve across the $x$x - axis by simply multiplying its function expression by $-1$−1.
Every function value of $y=-x^2$y=−x2 is the negative of those of $y=x^2$y=x2, and the curve becomes an upside-down parabola with the same vertex as $y=x^2$y=x2. Again, every function value of $y=-\frac{3}{x}$y=−3x is the reflected image of across the x -axis of $y=\frac{3}{x}$y=3x.
Combining Translations and dilations
When we combine translations and dilations we can reposition and distort the basic curve.
For example, the curve of $y=\frac{5}{x-2}+3$y=5x−2+3 is constructed as follows. Start with the curve given by the basic function $y=\frac{1}{x}$y=1x and stretch each ordinate by a factor of $5$5. Then shift it $2$2 units to the right and $3$3 units up, so that the centre becomes $\left(2,3\right)$(2,3) with the curve's asymptotes as $x=2$x=2 and $y=3$y=3.
The final graph is shown in red here, along with the graph of $y=\frac{1}{x-2}+3$y=1x−2+3. Note how changing from $y=\frac{1}{x-2}+3$y=1x−2+3 to $y=\frac{5}{x-2}+3$y=5x−2+3 pushes the hyperbola out diagonally.

Finding $x$x and $y$y intercepts
The $y$y intercept of any function are found by putting $x=0$x=0 into the equation. The $x$x intercept(s) are found similarly by putting $x=0$x=0.
For example, for the curve given by $y=\frac{1}{x-3}-5$y=1x−3−5, putting $x=0$x=0 reveals $y=\frac{1}{0-3}-5=-5\frac{1}{3}$y=10−3−5=−513.
The x intercept is found by putting $y=0$y=0, so that $\frac{1}{x-3}-5=0$1x−3−5=0. This means that $\frac{1}{x-3}=5$1x−3=5 and inverting $x-3=\frac{1}{5}$x−3=15 so that $x=3\frac{1}{5}$x=315.
Worked Examples
Question 1
Consider the equation $y=-2x$y=−2x.
Find the $y$y-value of the $y$y-intercept of the line.
Find the $x$x-value of the $x$x-intercept of the line.
Find the value of $y$y when $x=2$x=2.
Plot the equation of the line below.
Loading Graph...
Question 2
Consider the function $y=-\frac{1}{2}x^2$y=−12x2
Complete the following table of values.
$x$x $-2$−2 $-1$−1 $0$0 $1$1 $2$2 $y$y $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Plot the graph.
Loading Graph...
Question 3
Consider the cubic function $y=4x^3-3$y=4x3−3
Is the cubic increasing or decreasing from left to right?
Increasing
ADecreasing
BIs the cubic more or less steep than the function $y=x^3$y=x3 ?
More steep
ALess steep
BWhat are the coordinates of the point of inflection of the function?
Inflection ($\editable{}$, $\editable{}$)
Plot the graph $y=4x^3-3$y=4x3−3
Loading Graph...
Question 4
Consider the function $y=-\frac{1}{4x}$y=−14x
Complete the following table of values.
$x$x $-3$−3 $-2$−2 $-1$−1 $1$1 $2$2 $3$3 $y$y $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Sketch the graph.
Loading Graph...In which quadrants does the graph lie?
$1$1
A$2$2
B$3$3
C$4$4
D
