To form an equation of a sine or cosine curve from a graph or given information we need to identify the key features of the cyclic function. Once we have the key features identified we can construct the general form of the equations. Namely:
$f\left(x\right)=a\sin\left(bx-c\right)+d$f(x)=asin(bx−c)+d or $f\left(x\right)=a\cos\left(bx-c\right)+d$f(x)=acos(bx−c)+d
| vertical translation | Find the central point of the function, an imaginary line that the function appears to oscillate around. This is the value of $d$d in the general form of the equation. |
| amplitude | The maximum deviation of the function from the central line. This is the value of $a$a in the general form of the equation. |
| period | The length of one complete cycle. The value of the period is equal to $\frac{2\pi}{b}$2πb. We will use this and some algebra to determine the value of $b$b for the general form of the equation. |
| phase shift | Is there a horizontal translation? If so, then there is a phase shift of the function. The phase shift is equal to $\frac{c}{b}$cb. We will use this, and some algebra and the value of $b$b that we determined from the period to find the value of $c$c for the general form of the equation. |
| reflection | If there is a reflection, then the sine curve starts at the central line but decreases, and the cosine curve starts at the minimum and increases. If there is a reflection, then you make the value of $a$a negative. |
Worked Examples
Example 1
Find the equation of the cosine curve that has undergone the following transformations:
- a vertical translation of $4$4 units up
- a vertical dilation by a multiple of $2$2
- a horizontal translation resulting in a phase shift of $\frac{\pi}{4}$π4 units left
- a horizontal dilation by a multiple of $\frac{1}{2}$12
Think:
The general form of the cosine equation is $f\left(x\right)=a\cos\left(bx-c\right)+d$f(x)=acos(bx−c)+d, for which we need values of $a,b,c$a,b,c and $d$d. If we start by considering the $5$5 types of transformations and the values that they relate to we can determine the values of $a,b,c$a,b,c and $d$d for this equation.
Do:
| vertical translation | we are told $4$4 units up | $d=4$d=4 |
| amplitude | we are told a vertical dilation of a multiple of $2$2 | $a=2$a=2 |
| period | we are told a horizontal dilation by a multiple of $\frac{1}{2}$12, so the period changes from being $2\pi$2π in length to just half that which is $\pi$π in length. | $\frac{2\pi}{b}=\pi$2πb=π so $b=2$b=2 |
| phase shift | we are told a horizontal translation by $\frac{\pi}{4}$π4 units left. we also know that phase shift =$\frac{c}{b}$cb (remember that left is negative) | $\frac{c}{b}=-\frac{\pi}{4}$cb=−π4 so $c=-\frac{\pi}{2}$c=−π2 |
| reflection | there is no reflection, so the value of $a$a will be positive |
Putting all this together into the general form we determine the equation.
$f\left(x\right)=a\cos\left(bx-c\right)+d$f(x)=acos(bx−c)+d becomes $f\left(x\right)=2\cos\left(2x+\frac{\pi}{2}\right)+4$f(x)=2cos(2x+π2)+4
Example 2
Find the equation of the sine curve in the graph below.

Think:
The general form of the sine equation is $f\left(x\right)=a\sin\left(bx-c\right)+d$f(x)=asin(bx−c)+d, for which we need values of $a,b,c$a,b,c and $d$d. I start by marking on the diagram all the detail I can see that will help me. Namely, the period, central line, amplitude, any noticable reflection or any phaseshift.
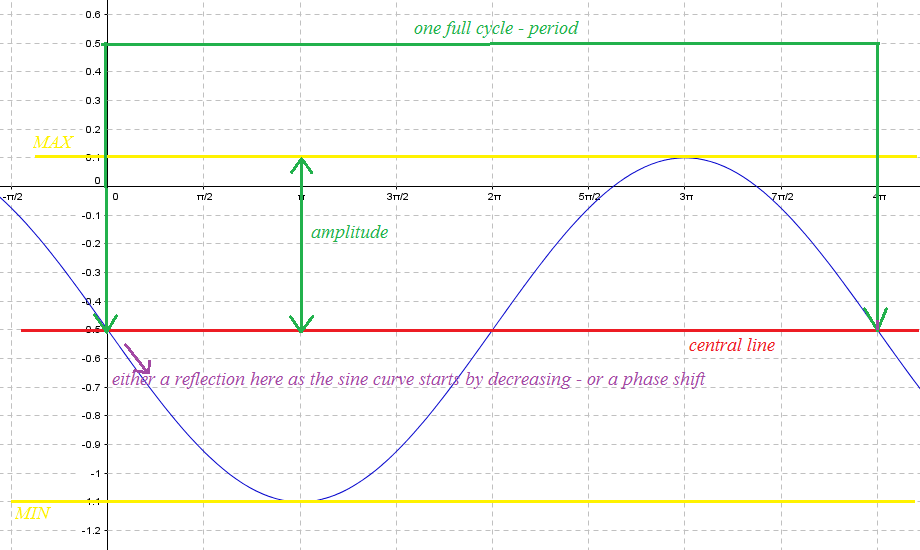
When finding equations we can sometimes get confused about whether there is a reflection or a phaseshift. Unless we are given specific information to check which applies, we will assume a phase shift has occurred.
Do:
| vertical translation | we can see in the diagram this is $0.5$0.5 units down. | $d=-0.5$d=−0.5 |
| amplitude | we can see the amplitude is $0.6$0.6 units | $a=0.6$a=0.6 |
| period | we can see on the graph that one full cycle takes $4\pi$4π | $\frac{2\pi}{b}=4\pi$2πb=4π so $b=\frac{1}{2}$b=12 |
| phase shift | As a sine curve normally starts by increasing from the central line, we can see that there is a phase shift here of $2\pi$2π units. | $\frac{c}{b}=2\pi$cb=2π so $\frac{c}{\frac{1}{2}}=2\pi$c12=2πso $c=\pi$c=π |
| reflection | As we have assume a phase shift, we say there is no reflection. |
Putting all this together into the general form we determine the equation.
$f\left(x\right)=a\sin\left(bx-c\right)+d$f(x)=asin(bx−c)+d becomes $f\left(x\right)=0.6\sin\left(\frac{x}{2}+\pi\right)-0.5$f(x)=0.6sin(x2+π)−0.5
Practice Questions
QUESTION 1
Determine the equation of the graphed function given that it is of the form $y=a\sin bx$y=asinbx or $y=a\cos bx$y=acosbx, where $b$b is positive.
QUESTION 2
Determine the equation of the graphed function given that it is of the form $y=c+\cos x$y=c+cosx or $y=c+\sin x$y=c+sinx.
QUESTION 3
Determine the equation of the graphed function given that it is of the form $y=\cos\left(x-c\right)$y=cos(x−c), where $c$c is the least positive value.
What are the different ways that we can transform the graph of the sine or cosine function? Recall that a transformation can be described algebraically using the variables $a$a, $b$b, $c$c, and $d$d, where
$\sin\left(x\right)\text{ }\rightarrow\text{ }a\sin\left(bx-c\right)+d$sin(x) → asin(bx−c)+d
We read this as "$\sin\left(x\right)$sin(x) transforms into $a\sin\left(bx-c\right)+d$asin(bx−c)+d". In this lesson we will focus on the role of the variable $c$c in horizontal translations or phase shifts and how it works in conjunction with other transformations.
Worked examples
Example 3
The graph of $y=\cos x$y=cosx has been shifted $\frac{\pi}{6}$π6 radians to the right. State the equation of the new graph.
Think: A shift to the right is a horizontal translation, so we know the new graph will have an equation of the form $y=\cos\left(x-c\right)$y=cos(x−c). We need to determine the magnitude and sign of the variable $c$c.
Do: The graph of $y=\cos x$y=cosx crosses the $y$y-axis at $\left(0,1\right)$(0,1). Since the whole graph is shifted by $\frac{\pi}{6}$π6 radians to the right, this point will move to $\left(\frac{\pi}{6},1\right)$(π6,1). We can substitute these coordinates into the form of the new equation to obtain the value of $c$c.
| $y$y | $=$= | $\cos\left(x-c\right)$cos(x−c) | |
| $1$1 | $=$= | $\cos\left(\frac{\pi}{6}-c\right)$cos(π6−c) | (Substituting the point $\left(\frac{\pi}{6},1\right)$(π6,1)) |
| $0$0 | $=$= | $\frac{\pi}{6}-c$π6−c | (Using the fact that $\cos\theta=1$cosθ=1 when $\theta=0$θ=0) |
| $c$c | $=$= | $\frac{\pi}{6}$π6 | (Adding $c$c to both sides of the equation) |
In the final line we see that $c=\frac{\pi}{6}$c=π6 radians, so that the equation of the new graph is $y=\cos\left(x-\frac{\pi}{6}\right)$y=cos(x−π6).
Reflect: If the horizontal translation had been to the left, we would have found that $c=-\frac{\pi}{6}$c=−π6, so that the new graph would have the equation $y=\cos\left(x-\left(-\frac{\pi}{6}\right)\right)=\cos\left(x+\frac{\pi}{6}\right)$y=cos(x−(−π6))=cos(x+π6).
Example 4
Consider the graph of the form $f\left(x\right)=\sin\left(b\left(x+c\right)\right)$f(x)=sin(b(x+c)) shown below.
State the equation of the graph. Give your answer in the form where $c$c is the least positive value.
Think: Compared to the graph of $y=\sin x$y=sinx, the graph of $f\left(x\right)$f(x) has been "squashed" horizontally due to the period change caused by $b$b, and translated horizontally due to the phase shift caused by $c$c.
Do: To determine the period change, recall that $y=\sin x$y=sinx has a period of $2\pi$2π, so that one whole cycle covers $2\pi$2π radians along the $x$x-axis. This means that one whole cycle of $\sin bx$sinbx will cover $\frac{2\pi}{b}$2πb along the $x$x-axis. From the graph we can see that the period of $f\left(x\right)$f(x) is $\frac{2\pi}{3}$2π3, so $b=\frac{2\pi}{\frac{2\pi}{3}}=3$b=2π2π3=3.
Next, we see that the point $\left(0,0\right)$(0,0) on the graph of $y=\sin x$y=sinx has been translated to the point $\left(-\frac{\pi}{12},0\right)$(−π12,0) on the graph of $f\left(x\right)$f(x). This corresponds to a phase shift of $\frac{\pi}{12}$π12 radians to the left, which means the value of the variable $c$c is $\frac{\pi}{12}$π12.
Now we can combine the working above and state the equation of the graph as $f\left(x\right)=\sin\left(3\left(x+\frac{\pi}{12}\right)\right)$f(x)=sin(3(x+π12)).
Reflect: How would the value of $b$b and $c$c change if we were told that the equation of the graph had the form $\sin\left(bx+c\right)$sin(bx+c) instead of $\sin\left(b\left(x+c\right)\right)$sin(b(x+c))?
The form of an equation affects how the corresponding graph transforms.
$a\sin\left(x-c\right)$asin(x−c) has a phase shift of $c$c units to the right.
$a\sin\left(b\left(x-c\right)\right)$asin(b(x−c)) has a phase shift of $c$c units to the right.
$a\sin\left(bx-c\right)$asin(bx−c) has a phase shift of $\frac{c}{b}$cb units to the right.
Practice questions
Question 4
Determine the equation of the graphed function given that it is of the form $y=\sin\left(x-c\right)$y=sin(x−c), where $c$c is the least positive value.
Question 5
Determine the equation of the graph given that it is of the form $y=-\cos\left(x+c\right)-d$y=−cos(x+c)−d, where $c$c is the least positive value and $x$x is in radians.
Question 6
In Enns, the temperature is recorded every 6 hours for 48 hours.
Plot the data over a two-day interval, where $x=0$x=0 corresponds to 12am on Monday.
Loading Graph...Day/Time Temperature (°C) Day/Time Temperature (°C) Monday 12am $9$9 Tuesday 6am $16$16 Monday 6am $14$14 Tuesday 12pm $23$23 Monday 12pm $22$22 Tuesday 6pm $17$17 Monday 6pm $16$16 Wednesday 12am $9$9 Tuesday 12am $8$8 To model the data, choose the sine curve that passes through the points $P$P, $Q$Q, $R$R and $S$S.
Loading Graph...$7\sin\left(\frac{\pi}{12}\left(x-6\right)\right)+16$7sin(π12(x−6))+16
A$7\sin\left(\frac{\pi}{12}x\right)+16$7sin(π12x)+16
B$7\sin\left(\frac{\pi}{12}\left(x-6\right)\right)$7sin(π12(x−6))
C$14\sin\left(\frac{\pi}{12}\left(x-6\right)\right)+16$14sin(π12(x−6))+16
DGraph $f\left(x\right)$f(x), the function you found in part (b), together with the data.
Loading Graph...
