The unit circle definitions of the trigonometric functions begin with sine and cosine: other functions are derived from these.
We consider a point that moves on the unit circle centred at the origin of a coordinate system. The radius to the point makes an angle with the positive horizontal axis. We define the cosine of this angle to be the horizontal coordinate of the point and we define the sine of the angle to be the vertical coordinate of the point.
Further trigonometric functions are defined from the sine and cosine functions.
The tangent function is given by:
$\tan\theta=\frac{\sin\theta}{\cos\theta}$tanθ=sinθcosθ
The secant function is the reciprocal of the cosine function:
$\sec\theta=\frac{1}{\cos\theta}$secθ=1cosθ
The cosecant function is the reciprocal of the sine function:
$\csc\theta=\frac{1}{\sin\theta}$cscθ=1sinθ
The cotangent function is the reciprocal of the tangent function:
$\cot\theta=\frac{1}{\tan\theta}=\frac{\cos\theta}{\sin\theta}$cotθ=1tanθ=cosθsinθ
These functions are useful in more advanced work where they can lead to simpler notations than would be the case if only sine and cosine were available.
Example:
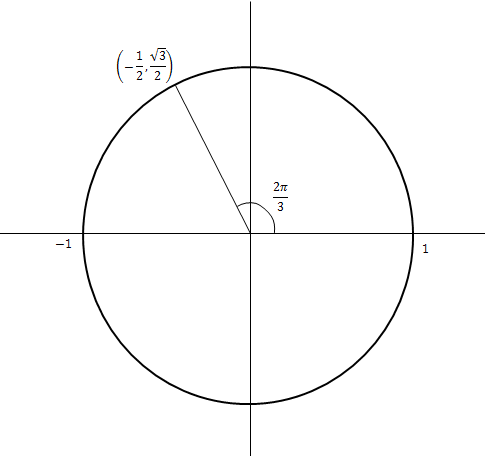
By reference to the diagram, give the values of each of the six trigonometric functions when $\theta=\frac{2\pi}{3}$θ=2π3.
From the coordinates we have:
$\cos\frac{2\pi}{3}=-\frac{1}{2}$cos2π3=−12 and $\sin\frac{2\pi}{3}=\frac{\sqrt{3}}{2}$sin2π3=√32
From these we find:
$\tan\frac{2\pi}{3}=-\sqrt{3}$tan2π3=−√3 , $\sec\frac{2\pi}{3}=-2$sec2π3=−2, $\csc\frac{2\pi}{3}=\frac{2}{\sqrt{3}}$csc2π3=2√3, and $\cot\frac{2\pi}{3}=-\frac{1}{\sqrt{3}}$cot2π3=−1√3.
Worked Examples
QUESTION 1
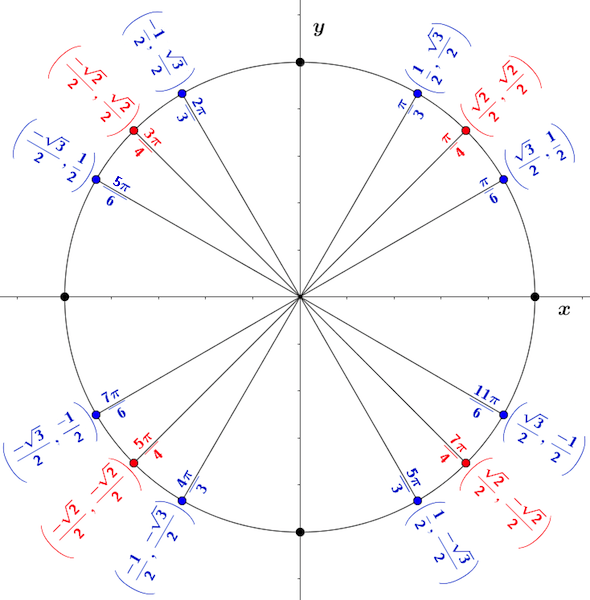
Use the figure to find the value of $\cos\left(-\frac{\pi}{6}\right)$cos(−π6).
QUESTION 2
Use the figure to find the value of $\sec\left(\frac{15\pi}{4}\right)$sec(15π4).

QUESTION 3
The graph shows an angle $a$a in standard position with its terminal side intersecting the circle at $P$P$\left(-\frac{21}{29},\frac{20}{29}\right)$(−2129,2029).
Find the value of $\sin a$sina.
Find the value of $\cos a$cosa.
Find the value of $\tan a$tana.