Think about the generating rule for a particular arithmetic progression given by $t_n=2n+3$tn=2n+3. We can cleverly rearrange this equation to $t_n=5+\left(2n-2\right)$tn=5+(2n−2) . By taking out common factors on the last two terms, the expression becomes:
$t_n=5+\left(n-1\right)\times2$tn=5+(n−1)×2
Comparing this to the general formula for the $n$nth term of an AP, given by $t_n=a+\left(n-1\right)d$tn=a+(n−1)d , we can immediately see that the first term is $5$5 and the common difference is $2$2.
Thus any generating rule of the form $t_n=dn+k$tn=dn+k where $d$d and $k$k are constants can be shown to be an arithmetic sequence. Just like the equation $y=mx+c$y=mx+c is drawn as a straight line, so the arithmetic progression given by $t_n=dn+k$tn=dn+k is plotted as a series of points that are all in a straight line.
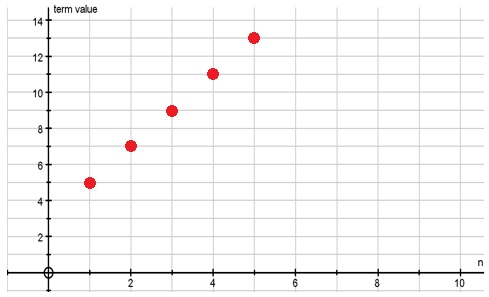
The first term is represented by the left-most point shown $\left(t_1=5\right)$(t1=5) . The slope of the marked points measured, as the vertical distance between the points, is the common difference. In our example, the line of points is rising, so this indicates a positive common difference. In other instances, the line might be falling and this would indicate a negative common difference.
In the example above, where , the common difference is immediately recognizable as the coefficient of . A simple way of finding the first term is to evaluate as . We could place these values in a table as follows:
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| tn | 5 | 7 | 9 | 11 | 13 |
Arithmetic sequences are said to grow linearly literally meaning ‘in a straight line’. We find applications of linear growth in many areas of life, including simple interest earnings, straight-line depreciation, monthly rental accumulation and many others. Whenever something grows or diminishes in constant quantities over equal time periods, then that growth or fall is said to be linear.
Worked Examples
QUESTION 1
The $n$nth term of an arithmetic progression is given by the equation $T_n=12+4\left(n-1\right)$Tn=12+4(n−1).
Complete the table of values.
$n$n $1$1 $2$2 $3$3 $4$4 $10$10 $T_n$Tn $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ By how much are consecutive terms in the sequence increasing?
Plot the points in the table on the graph.
Loading Graph...If the points on the graph were joined, they would form:
a straight line
Aa curved line
B
QUESTION 2
The plotted points represent terms in an arithmetic sequence:
Complete the table of values for the given points.
$n$n $1$1 $2$2 $3$3 $4$4 $T_n$Tn $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Identify $d$d, the common difference between consecutive terms.
Write a simplified expression for the general $n$nth term of the sequence, $T_n$Tn.
Find the $15$15th term of the sequence.
QUESTION 3
A racing car starts the race with $150$150 litres of fuel. From there, it uses fuel at a rate of $5$5 litres per minute.
What is the rate of change?
Fill in the table of values:
Number of minutes passed ($x$x) $0$0 $5$5 $10$10 $15$15 Amount of fuel left in tank in litres ($y$y) $150$150 $\editable{}$ $\editable{}$ $\editable{}$ Write an algebraic equation linking the number of minutes passed ($x$x) and the amount of fuel left in the tank ($y$y).
By rearranging the equation found in part (d), calculate how long it will take for the car to run out of fuel.