Scalar Multiplication
As a scalar is a quantity that is magnitude only (no direction), its affect on a vector when multiplying is to increase the magnitude of the vector. It does not alter its direction.
Scalar multiplication of vectors can be done geometrically (like in the applet above), where we draw the resulting vector with the scaled magnitude and same direction. But it can also be done algebraically using column vector notation.
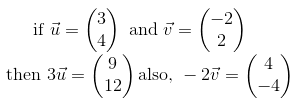
Note also how a negative scalar multiple is actually a negative of the vector (same magnitude opposite direction) and then it is scaled according to the scalar quantity.
Familiarise yourself with the behaviour of scalar multiplication.
c and d scalars, $v$v and $w$w vectors
- Left distributivity: $\left(c+d\right)v=cv+dv$(c+d)v=cv+dv
- Right distributivity: $c\left(v+w\right)=cv+cw$c(v+w)=cv+cw
- Associativity: $\left(cd\right)v=c\left(dv\right)$(cd)v=c(dv)
- Mutliplying by $1$1 does not change a vector: $1v=v$1v=v
- Multiplying by $0$0 gives the zero vector: $0v=0$0v=0
- Multiplying by $-1$−1 gives the additive inverse: $-1v=-v$−1v=−v
Construct examples (using diagrams and algebra), that demonstrate each of these properties.
Worked Examples
Question 1
Is $-2\left(5\vec{NM}\right)$−2(5→NM) equal to $10\vec{MN}$10→MN?
Yes
ANo
B
Question 2
| Let $p$p$=$= |
|
, $q$q$=$= |
|
, and $r$r$=$= |
|
. |
Find $6p$6p:
$6p$6p$=$= $\editable{}$ $\editable{}$ Find $q+r$q+r:
$q+r$q+r$=$= $\editable{}$ $\editable{}$ Find $mq-r$mq−r:
$mq-r$mq−r$=$= $\editable{}$ $\editable{}$ Find $p+q-r$p+q−r:
$p+q-r$p+q−r$=$= $\editable{}$ $\editable{}$
Question 3
Consider the vectors plotted on the graph.
Find $c-d$c−d.
$\editable{}$ $\editable{}$ Find $3a-b$3a−b.
$\editable{}$ $\editable{}$ Find $-4b+2c$−4b+2c.
$\editable{}$ $\editable{}$