
Finding Unknown Side Lengths Using Trig Ratios
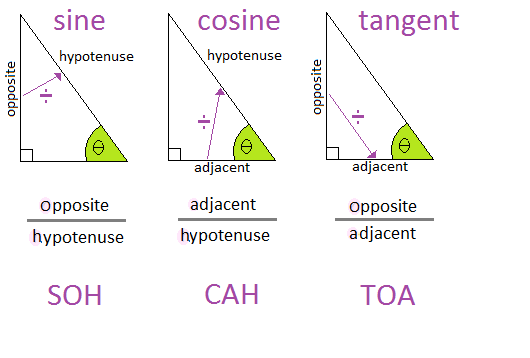
As we saw in our chapter on Special Ratios, there are 3 trigonometric ratios that relate an angle and sides together. They are:
$\sin\theta$sinθ = $\frac{Opposite}{Hypotenuse}$OppositeHypotenuse
$\cos\theta$cosθ = $\frac{Adjacent}{Hypotenuse}$AdjacentHypotenuse
$\tan\theta$tanθ = $\frac{Opposite}{Adjacent}$OppositeAdjacent
If we know any $2$2 parts of a right-angled triangle, whether that's $2$2 side lengths, or an angle and a side length we can then find any other part of that triangle using these trigonometric ratios.
Finding Side lengths
If we know $2$2 sides and want to find the third, we would use pythagorean formula
$a^2+b^2=c^2$a2+b2=c2
If we know 1 side length and an angle, we would use one of the trigonometric ratios.
The most common mistake is when the wrong ratio is used. We have to remember the ratios and the sides that apply to those ratios. For most students the mnemonic SOHCAHTOA can be a great help.
Examples
Question 1

In the given triangle $\theta=25^\circ$θ=25° and the hypotenuse measures $12.6$12.6. Solve for the length $b$b.
Think: We need to identify the sides we have and want with respect to the angle given. Here I can see that we have the hypotenuse (H) and we want $b$b, which is opposite (O) the angle. This means I have OH - so the trig ratio I need to use here is sine.
Do:
| $\sin\theta$sinθ | $=$= | $\frac{O}{H}$OH |
| $\sin25^\circ$sin25° | $=$= | $\frac{b}{12.6}$b12.6 |
| $b$b | $=$= | $12.6\times\sin25^\circ$12.6×sin25° |
| $b$b | $=$= | $5.32$5.32 |
Question 2
Find the length of the hypotenuse ($c$c) in the diagram, where the angle $36^\circ$36° and the side length of $4.8$4.8 are given.

Think: We need to identify the sides we have and want with respect to the angle given. Here I can see that we want the hypotenuse (H) and we have a side length of $4.8$4.8, which is adjacent (A) the angle. This means I have AH - so the trig ratio I need to use here is cosine.
Do:
| $\cos\theta$cosθ | $=$= | $\frac{A}{H}$AH |
| $\cos36^\circ$cos36° | $=$= | $\frac{4.8}{c}$4.8c |
| $c$c | $=$= | $\frac{4.8}{\cos36^\circ}$4.8cos36° |
| $c$c | $=$= | $5.93$5.93 units (to 2 d.p.) |
Question 3
Find the length of the unknown side, when the angle is $66^\circ$66° and the indicated side length is $7.3$7.3.

Think: We need to identify the sides we have and want with respect to the angle given. Here I can see that we want the adjacent side (A) and we have a side length of $7.3$7.3, which is opposite (O) the angle. This means I have OA - so the trig ratio I need to use here is tangent.
Do:
| $\tan\theta$tanθ | $=$= | $\frac{O}{A}$OA |
| $\tan66^\circ$tan66° | $=$= | $\frac{7.3}{a}$7.3a |
| $a$a | $=$= | $\frac{7.3}{\tan66^\circ}$7.3tan66° |
| $a$a | $=$= | $3.25$3.25 units (to 2 d.p.) |
Question 4
Find the value of $f$f, correct to two decimal places.

Question 5
Find the value of $h$h, correct to two decimal places.

Question 6
Find the value of $x$x, the side length of the parallelogram, to the nearest centimetre.

A parallelogram with its angle at upper-right corner labeled as 52 degrees, indicating its measure. Other angles of the parallelogram are not labeled. Its top side is labeled 32 cm, indicating its length. Its left side is labeled $x$x cm, indicating its unknown length. A perpendicular internal segment is drawn from the upper-left corner to the bottom side of the parallelogram, thus creating a right-angled triangle on the left side. The bottom side of the parallelogram, which is parallel to the top side as indicated by the double arrowheads, is cut into two parts: the left part with no measurement indicated and the right part which measures 11 cm, as labeled.
In the triangle, the sides are the internal segment, the left side of the parallelogram, and the left part of the bottom side of the parallelogram. A square symbol is shown at the corner where the internal segment and the bottom side intersect to indicate that it is a right angle. The left side of the parallelogram labeled $x$x cm acts as the hypotenuse of the triangle. The internal segment is the vertical leg of the triangle. The left part of the bottom side of the parallelogram acts as horizontal leg of the triangle.