
Area of Rectangles and Triangles
Areas of Rectangles
A rectangle is a shape with the specific geometric properties of
- opposite sides equal in length
- opposite sides parallel
- sides meet at right angles.
To determine the area of a rectangle we divide the rectangle up into square units and count them up.
Here is a rectangle measuring $4$4 units in length and $2$2 units in width.
 |
We divide the rectangle up into its square units and see how many there are |
 |
This rectangle has an area of 8 square units. |
How did we get 8? Well, we could count the squares $1$1 at a time. Or we could use multiplication by seeing that there are $2$2 rows of $4$4, ($2\times4=8$2×4=8) or that there are $4$4 columns of $2$2 ($4\times2=8$4×2=8). Did you notice? These were the lengths of the sides.
This is great, it looks like we have found a simple way of finding the area of rectangles. We turn the rectangle into an array based on the lengths of the sides and multiply.
See these:
 |
$1\times4$1×4 | rectangle has area of | $1\times4=4$1×4=4 square units |
 |
$2\times3$2×3 | rectangle has area of | $2\times3=6$2×3=6 square units |
 |
$6\times3$6×3 | rectangle has area of | $6\times3=18$6×3=18 square units |
Of course we don't have to draw in all the little squares every time. Now that we understand the array structures within rectangles we can just use the rule to find the area of a rectangle.
$\text{Area of a Rectangle }=\text{length }\times\text{width }$Area of a Rectangle =length ×width
$A=L\times W$A=L×W
Knowing the area of a rectangle is a very powerful thing! As you will see in the next few chapters, areas of rectangles will help us find the areas of squares, triangles, parallelograms, trapeziums and even more!
Area of Squares
A square is a shape with the specific geometric properties of
- opposite sides equal in length
- opposite sides parallel
- sides meet at right angles
AND
- all sides equal.
This makes a square a very special kind of rectangle, because it meets all the requirements of a rectangle but has one extra special geometric property.
To find the area of a square, we use the rectangle rule,
$A=L\times W$A=L×W
but because the $L$L and $W$W are the same, then the area of a square is just
$\text{Area of a Square }=\text{Side }\times\text{Side }$Area of a Square =Side ×Side
$A=S\times S$A=S×S
See these squares
 |
Area | $=$= | $3\times3$3×3 | |
| $=$= | $9$9 square units | |||
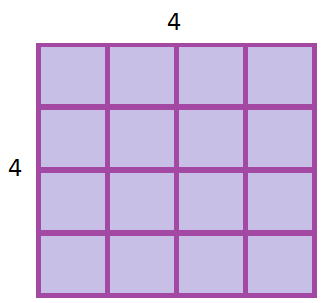 |
Area | $=$= | $4\times4$4×4 | |
| $=$= | $16$16 square units |
Units
We use special units to describe area, based on the notion of square units described above. Because the units for length include millimetres, centimetres, metres and kilometres we end up with the following units for area.
square millimetres = mm2
(picture a square with side lengths of $1$1 mm each - pretty small this one!)
square centimetres = cm2
(picture a square with side lengths of $1$1 cm each - about the size of a fingernail)
square metres = m2
(picture a square with side lengths of $1$1 m each - what do you know that is about this big?)
square kilometres = km2
(picture a square with a side length of $1$1km - I wonder how many of these your town or city is?)
TRIANGLES
Did you know a rectangle can be drawn around every single triangle. See these:



But what is really amazing about these constructions is that the area of the triangle is exactly equal to the area of the extra triangles we added to make the rectangles!
Check out the mathlet below to see for yourself. Drag the vertices of the triangle to change its shape and then slide the slider to see how it turns into a rectangle.
Why does this matter?
Well we already know how to find the area of a rectangle ($A=L\times W$A=L×W), and the interactive above shows us that the triangle is half of that!
This means that the
$\text{area of a triangle }=\text{half of the area of the rectangle with base and height the same as the triangle }$area of a triangle =half of the area of the rectangle with base and height the same as the triangle
$\text{area of a triangle }=\frac{1}{2}\times\text{base }\times\text{height }$area of a triangle =12×base ×height
$A=\frac{1}{2}bh$A=12bh