We have already seen what the trigonometric ratios are,
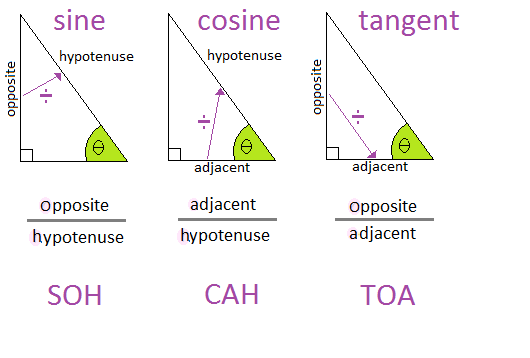
We know how to calculate with them, and how to find the length of unknown sides of right-angled triangles with them.
- Construct a triangle that represents the given situation, labelling all known values
- Label the sides as O, A or H with respect to the position of the known angle
- Identify the appropriate trigonometric ratio that applies [either sine (sin), cosine (cos) or tangent (tan)]
- Using algebra, solve the equation for the angle, (write the rule, fill in what you know, then rearrange to solve for the unknown side length)
- Reflect and check (do a quick check on your calculator to confirm your answer is correct)
We have also seen how to use the trigonometric ratios to find the size of unknown angles. To do this we need any $2$2 of the side lengths.
- Construct a triangle that represents the given situation, labelling all known values
- Label the sides as O, A or H with respect to the position of the angle you want to find
- Identify the appropriate trigonometric ratio that applies [either sine (sin), cosine (cos) or tangent (tan)]
- Using algebra, solve the equation for the angle, (write the rule, fill in what you know, then solve using inverse operations)
- Reflect and check (do a quick check on your calculator to confirm your answer is correct)
Practice questions
Question 1
The person in the picture sights a paraglider above him.
If the angle the person is looking at is $a$a, find $a$a to two decimal places.

Question 2
If $d$d is the distance between the base of the wall and the base of the ladder, find $d$d to two decimal places.

Question 3
Jack is standing at the tip of a tree's shadow and knows that the angle from the ground to the top of the tree is $34^\circ$34°.
If Jack is standing $29$29 metres away from the base of the tree, what is the value of $h$h, the height of the tree to the nearest two decimal places?