Interpretion of Data with Awareness of Issues (Investigation)
In this discussion, we consider data that is generated by taking measurements on a set of subjects that have been given various amounts of some treatment.
A researcher might need to handle data of this kind when trying to discover whether changing the amount of a treatment has an effect on the subject. If there is no noticeable effect when the treatment level is varied, then there is no evidence that the treatment affects the response.
For example, an agricultural scientist might try applying different amounts of a new fertilizer to separate plots within a wheat crop. The treatment is the fertilizer and the subject is the wheat. If there are only random differences in the amount of growth measured in the separate plots of wheat, then the scientist might conclude that varying the amount of fertilizer does not explain variations in the growth in the wheat plots.
The words treatment and response are used both for experimental situations where the treatment can be deliberately varied and also for observational studies where naturally occurring variations in one quantity might be found to be related to variations in another.
Often, what is called a treatment might have to be just a naturally occurring variation, like a person's weight. In medical research, for example, it would be unethical to deliberately manipulate a patient's weight in order to see what effect this had on his or her heart rate. But, a large number of subjects having various weights could be observed and their heart rates measured, and the different weights would be considered as treatments.
So, we consider the relation between a treatment variable and a response variable. The data will consist of pairs of numbers (a,b) where the first number a is the level of a treatment for one of the subjects and the second number b is the observed response measurement.
After collecting the data, the pairs of numbers can be displayed in a scatterplot.
Example 1
For the purposes of illustration, it does not matter what the experiment was. For the moment, we are only interested in the data. Suppose the treatment levels were 1, 2, 3, 4, 5 and there were three trials at each level. That is, three subjects were observed at each treatment level so that 15 data points were collected in all.
| 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 |
| 6 | 5.5 | 6.5 | 9 | 11 | 10 | 12 | 16 | 14 | 18.5 | 17.5 | 19 | 19 | 21 | 26 |
By convention, the treatment variable is measured along the horizontal axis and the corresponding responses are on the vertical axis.
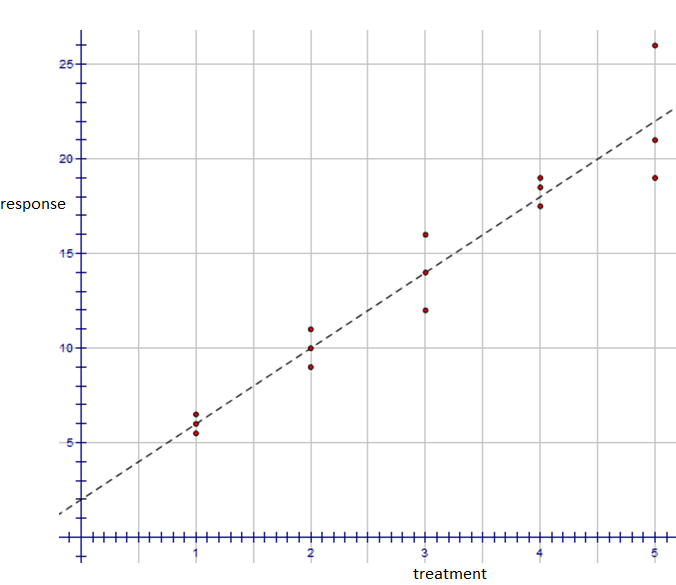
In this example, it is clear from the plot that the response is related to the treatment level. The data points appear to be clustered around a line.
The line is called a regression line. It is the line that comes closest to all of the data points and is often called a line of best fit. The regression line predicts approximately what the response will be in a future experiment given some treatment level. The researcher's next step would be to work out the formula for the regression line.
Data points are not always so clearly clustered around a regression line. There will be a line of best fit in every case but it may not be a good predictor of future results when the observed responses are scattered with no clear trend or pattern.
Example 2
The following pairs of measurements were obtained from an observational study.
(12.5, 24), (14, 23.5), (14.4, 24.5), (15.3, 21), (15.7, 22.5), (16.1, 24.5), (16.5, 25.5), (17.2, 26), (18, 25.9), (18.5, 26.5), (19.5, 21).
The following scatterplot displays this data.
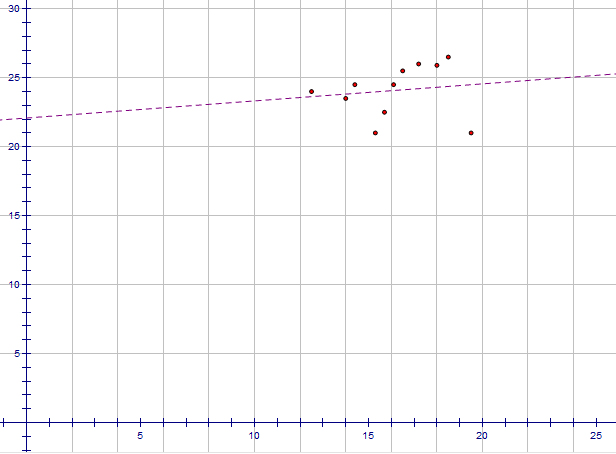
It is still possible to insert a line of best fit. There are technical methods for doing this. However, the plot suggests that the response changes very little and unpredictably with changes in the treatment level.
Activity
The process of collecting and analysing data begins with a hypothesis. An experiment or an observational study is then carried out carefully to test the hypothesis.
To complete this investigation, you should propose your own hypothesis and design a study to test it. The following is only a suggestion. You might have other ideas.
For example, suppose you wish to test the theory that a person's handspan has an effect on their typing speed when composing text messages.
Having decided on the hypothesis you wish to test, you should select your experimental subjects, carry out the appropriate measurements and display the data as a scatter plot.
Spreadsheet applications like Excel can be used to automate the creation of a scatter plot and will insert a regression or trend line and provide its formula.
There are things to be aware of and to be avoided in this and any other study.
bias
One should not include only expert texters in the study as this could introduce a bias. Any conclusions would only relate to people who fell into the category of expert texters and not to the general population. Instead, subjects for the experiment should be randomly selected so that they do reflect the abilities of the population.
It may be that certain groups could be expected to have differing texting abilities for religious or cultural reasons. There could be people with no experience of mobile telephones, for example. These people would introduce a factor to the experiment that could confuse the results.
The experimenter should be aware that the conclusions reached can only apply to the actual population from which the subjects were selected. The experiment can say nothing definite about classes of people who were not adequately represented in the data.
ethics
Some subjects might be sensitive about their handspan or about their texting ability. You should make sure individual subjects cannot be identified in the data. Usually, the names of subjects in an experiment or survey are kept separately from the measurements they provide.
It may be that a person you selected to be a subject in your experiment has an objection to having their handspan measured. Some may be unable to participate for medical reasons.
In such a case, you would need to replace the subject with someone else selected randomly from the population you are testing.