Domain and Range of Absolute Value Functions II

For any function, we understand the domain to be the set of values that the independent variable can take. The range is the image of the domain values under the effect of the function.

Absolute value functions of the form $|f(x)|$|f(x)| are defined on some subset of the real numbers, their domain, and this subset is mapped by the function into the non-negative real numbers. Thus, the range of an absolute value function of this form is a subset of the positive numbers.  

A simple function of this form can be subjected to further shifts and reflections that may result in negative values appearing in the range. For example, $-|f(x)|$−|f(x)| is always negative, and $A-|f(x)|$A−|f(x)| is negative for $|f(x)|>A$|f(x)|>A.

Linear examples

The absolute value function applied to linear functions produces graphs made of line segments. 

Thus, for example, $y=|x-4|$y=|x−4| is a combination of $y=4-x$y=4−x when $x\le4$x≤4, and $y=x-4$y=x−4 when $x>4$x>4. The natural domain, in this example, is the whole of the set of real numbers. The function maps the domain into the real numbers but, more precisely, the image or range of the function is the set of numbers greater than or equal to zero.

Applying a vertical shift and a reflection to the same function, we might ask for the domain and range of, say, $y=5-|x-4|$y=5−|x−4|. The domain is the set of real numbers, as before, but in this case, the range includes both positive and negative numbers. 

The maximum value the function can take is $5$5, when $|x-4|=0$|x−4|=0. That is, when $x=4$x=4. 

The two parts of the function are, thus, $y=x+1$y=x+1 when $x\le4$x≤4 and $y=9-x$y=9−x when $x>4$x>4.

The function has the value zero when $|x-4|=5$|x−4|=5. This occurs when $x=9$x=9 and when $x=-1$x=−1. Between these domain values, the function is positive and it is negative otherwise. The function can be made as large in the negative direction as we wish by making $|x-4|$|x−4| arbitrarily large.

Thus, the range is the set $y\le5$y≤5.

quadratic examples

The absolute value function applied to quadratic functions produces graphs made of parabolic arcs.

The function given by $p(x)=x^2+2x-3$p(x)=x2+2x−3 has zeros at $x=1$x=1 and $x=-3$x=−3. Between these domain values, the function is negative and it is positive elsewhere. Thus, the critical points of the absolute value function $q(x)=|x^2+2x-3|$q(x)=|x2+2x−3| are at $x=1$x=1 and $x=-3$x=−3.

We can write $q(x)$q(x) as a combination of $q(x)=-p(x)$q(x)=−p(x) for $-3\le x\le1$−3≤x≤1 and $q(x)=p(x)$q(x)=p(x) elsewhere.

The natural domain is the set of real numbers and the range is the set of non-negative real numbers.

 

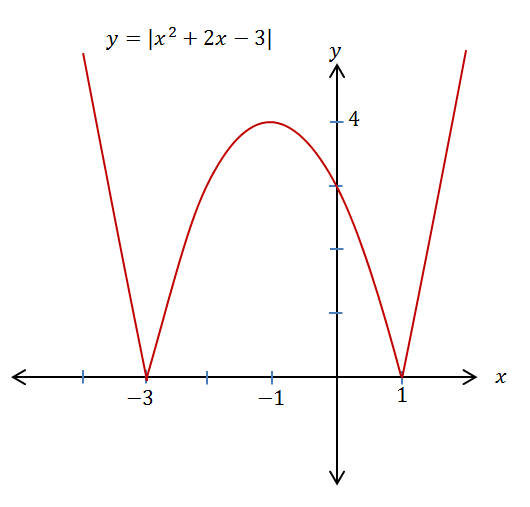
From $q(x)$q(x), we might construct another function, $r(x)=A-q(x)$r(x)=A−q(x). As in the linear example, the constant $A$A shifts the graph vertically and the negative sign reflects the graph about the line $q(x)=A$q(x)=A.

 

We might further complicate the construction by applying the absolute value function to just the linear part of $p(x)$p(x). Thus, we could have $y(x)=x^2+|2x-3|$y(x)=x2+|2x−3|.

As before, the domain can be all of the real numbers. The function maps the domain into the non-negative real numbers because both $x^2$x2 and $|2x-3|$|2x−3| are always non-negative. The function value can be made very large by allowing $x$x to be sufficiently large but we also wish to know the minimum value of the function in order to specify the range.

A critical value occurs where $|2x-3|=0$|2x−3|=0. That is, at $x=\frac{3}{2}$x=32​. For $x\le\frac{3}{2}$x≤32​, the function can be written $y_1(x)=x^2-2x+3$y1​(x)=x2−2x+3, and for $x>\frac{3}{2}$x>32​ we have $y_2(x)=x^2+2x-3$y2​(x)=x2+2x−3.

Now, $y_2$y2​ has zeros at $x=-3$x=−3 and $x=1$x=1 and a minimum between these values that must be less than zero. This minimum is not in the domain of definition of $y_2$y2​. So, the minimum we seek must be the minimum of $y_1$y1​.

The quadratic $y_1$y1​ is never negative. By completing the square, we can rewrite it as $y_1(x)=x^2-2x+1+2=(x-1)^2+2$y1​(x)=x2−2x+1+2=(x−1)2+2. This expression is at its smallest when $x-1=0$x−1=0. That is, when $x=1$x=1, which is within the domain of $y_1$y1​.

At this point, $y(x)=2$y(x)=2. Hence, we conclude that the range of $y(x)=x^2+|2x-3|$y(x)=x2+|2x−3| is $y\ge2$y≥2.

 

 

More worked examples

Question 1

Question 2

Question 3