Applications of Bearings
Example 1

A slightly lost hiker walks $300$300 m east before turning south walking another $800$800 m. What is its true bearing from its original position (to $1$1 decimal place)? And then what is this as a compass bearing?
Think: to do this questions a diagram is a great way to start. This is the diagram I drew.
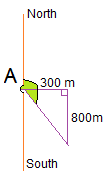
The angle we want to find is in green. It is equal to 90° + the angle inside the triangle that I can find using trigonometry.
Do: Bearing is
| $90+\tan^{-1}\frac{800}{300}$90+tan−1800300 | $=$= | $90+\tan^{-1}\frac{8}{3}$90+tan−183 |
| $=$= | $90+69.44$90+69.44 | |
| $=$= | $159.44$159.44 |
and to 1 decimal place the final bearing is $159.4$159.4°N
As a compass bearing we need to know the acute angle with the North South line. This is $180-159.4=20.6$180−159.4=20.6
The compass points we will use will be South first, and then East, so the compass bearing is S$20.6$20.6°E
Example 2
The position of a ship S is given to be $20$20 kilometres from P, on a true bearing of $0$0$49$49$^\circ$°T.
The position of the ship can also be given by its $\left(x,y\right)$(x,y) coordinates.

If the ship's $x$x-coordinate is $x$x, find $x$x to one decimal place.
If the ship's y-coordinate is $y$y, find $y$y to one decimal place.