Length Units and Conversions
Big steps or little?
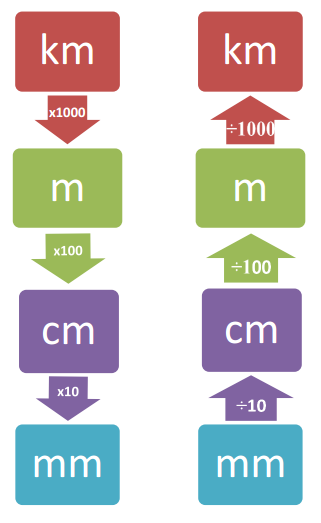
If we need to convert a length from kilometres (km) to centimetres (cm), we could do it in one big step. This is like jumping from one side of the creek to the other. We could also do this in smaller steps, a bit like using stepping stones to cross the creek. This gives us some support, and reduces the chance of us falling in!
We've converted lengths to the next smaller (or bigger) measurement, so let's see how we can use this to convert to a measurement that is even smaller, or bigger.
More steps?
What if we need to convert a length from millimetres (m) to kilometres (km)? How could you do this? Think about the units of measurement between mm and km, and how we might do this. How many steps could you take?
Be sure to know when to multiply, and when to divide. If we are converting to smaller units (such as from km to m), we end up with much smaller units, but more of them. That means we need to multiply our number. It is really useful to know when to multiply, and when to divide, but this image is is very useful to use.
Worked Examples
Question 1
Convert $6.22$6.22 km to cm.
$6.22$6.22 km = $\editable{}$ cm
Question 2
Convert $512200$512200 cm to km. Write your answer as a decimal.
$512200$512200 cm = $\editable{}$ km
Question 3
Convert $2.12$2.12 km to mm.