Introduction to Circles
When we looks at graphs of functions or relations, we concentrate our focus on key characteristics of a graph.
For example, when we look at a parabola of a quadratic function, we might focus on the turning point or the $x$x intercepts.
If we examine the graph of a hyperbola, we'll concentrate our focus on the intersection of the vertical and horizontal asymptote.
Now we're interested in examining the graph of a circle, and to do that we need to concentrate our focus on two key characteristics.
Characteristics of a Circle Graph
If you were to guess what a key feature of a circle might be, what would you say?
Probably the radius. This is certainly a key feature which we'll need to focus on for these graphs.
The other feature, which you might not guess, is the coordinate of the centre of the circle.
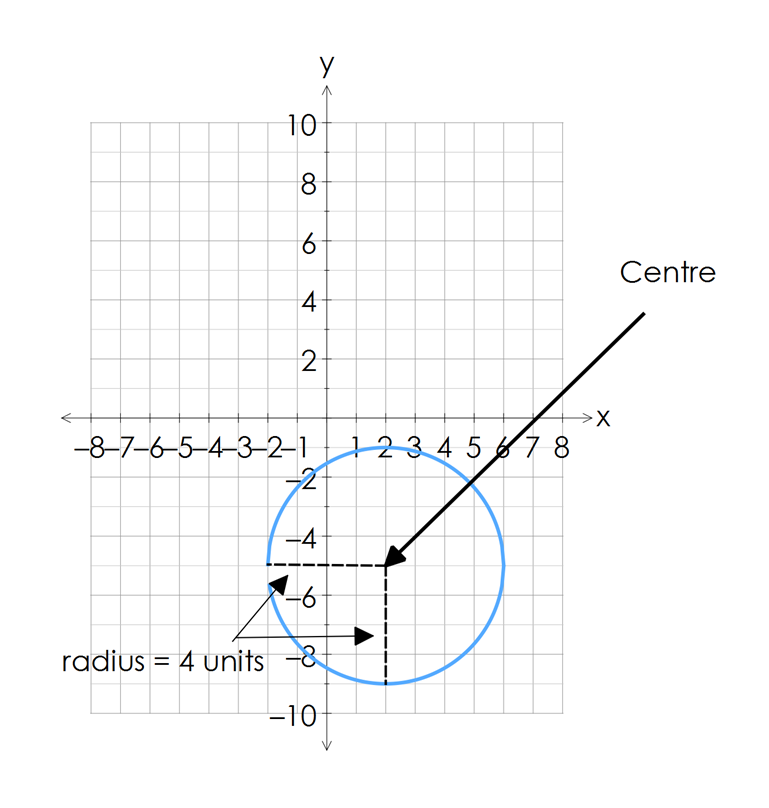
On the graph below, you can see, by inspection, that the centre of the circle is $(2,-5)$(2,−5)
We can determine the radius of the circle by counting the number of units from the centre, out to the left or right of the centre, or directly up or down from the centre. So for this graph the radius is $4$4 units.
Worked Examples
QUESTION 1
Consider the following.
Plot four points such that they are all exactly $4$4 units away from the origin.
Loading Graph...Considering the four points plotted in the previous part, what shape is formed by connecting the points with four straight paths?
triangle
Aquadrilateral
Bcircle
CAs the number of points we plot and connect increases towards infinity, what shape do we approach?
octagon
Acircle
Bdecagon
C
QUESTION 2
Consider the circle in the graph.
A two-dimensional Cartesian coordinate system with axes labeled $x$x and $y$y, both ranging from $-7$−7 to $7$7. A circle is plotted, with a solid line outlining its circumference. Points $\left(1,2\right)$(1,2), $\left(1,-6\right)$(1,−6), $\left(-3,-2\right)$(−3,−2), and $\left(5,-2\right)$(5,−2) are points on the circumference of the circle. However, these points are not explicitly labeled or given. Point $\left(1,2\right)$(1,2) is the top-most point on the circle. Point $\left(1,-6\right)$(1,−6) is the bottom-most point on the circle. Point $\left(-3,-2\right)$(−3,−2) is the left-most point on the circle. Point $\left(5,-2\right)$(5,−2) is the right-most point on the circle.
State the coordinates of the centre in the form $\left(a,b\right)$(a,b).
State the diameter.