
Adding and Subtracting Mixed Numbers
Fractions pop up in so many different places everyday. We use fractions when dealing with decimals, percentages, rates, ratios, lengths, distances and so on. When figuring out anything from how much change we get at the shop to cutting a cake to simply measuring things, fractions play an important part in our understanding of how many parts anything can be divided into.
Proper fractions
A fraction is considered proper, if it is of the form $\frac{A}{B}$AB and $A
This means that if a fraction does not have this form it is either Mixed OR Improper.
Improper fractions
A fraction is called improper if the top number (numerator) is larger than the bottom number (denominator). That makes it of the form $\frac{A}{B}$AB where $A>B$A>B.
So the following are all improper fractions,
$\frac{47}{46}$4746, $\frac{110}{43}$11043, $\frac{7}{4}$74, $\frac{11}{3}$113 and so on.
Adding and subtracting improper fractions
Adding and subtracting improper fractions is exactly the same process as adding and subtracting other types of fractions like we did here in Adding Parts . It might look a little different and the numbers might get bigger than you're used to, but it's all the same!
Example
Question 1
Evaluate: $\frac{9}{4}+\frac{6}{5}$94+65
Think: Find the LCM between $4$4 and $5$5 and find equivalent fractions. Then we will be able to add them.
Do: The LCM between $4$4 and $5$5 is $20$20.
| $\frac{9}{4}+\frac{6}{5}$94+65 | $=$= | $\frac{45}{20}+\frac{24}{20}$4520+2420 |
| $=$= | $\frac{69}{20}$6920 |
Mixed numbers
A fraction is called a mixed number if it is a combination of whole numbers and fractions.
The following are examples of mixed numbers.
$1$1 $\frac{2}{3}$23, $14$14$\frac{5}{7}$57, $14$14$\frac{3}{5}$35
Adding and subtracting mixed fractions
There are two ways of looking at adding or subtracting mixed numbers.
Method 1 - Using improper fractions
The first idea is to convert the mixed number into an improper fraction and then add or subtract as we do normally.
A number like this $1\frac{2}{3}$123 means $1$1 whole and $\frac{2}{3}$23. To turn this into an improper fraction you need to work out how many thirds there are in $1$1 whole and $\frac{2}{3}$23 altogether. Well there are $3$3 thirds in a whole, so altogether we have $5$5 thirds, $\frac{5}{3}$53.
$14\frac{5}{7}$1457 means $14$14 wholes and $\frac{5}{7}$57. To turn this into an improper fraction you need to work out how many sevenths there are altogether in $14$14 wholes and $\frac{5}{7}$57. Well, $14$14 wholes is $14\times7$14×7 sevenths, which is $98$98 sevenths. Altogether then we have $98+5$98+5 sevenths which is $\frac{103}{7}$1037.
For any mixed number we can turn it into an improper fraction by thinking about it in this way.
Once it is in the form of an improper fraction you can add and subtract as we did before.

Converting a mixed numeral to an improper fraction
or more generally...

General form of converting to an improper fraction
Method 2 - Dealing with wholes and parts separately
Consider the question $2\frac{1}{5}+1\frac{1}{4}$215+114
What we have here is:
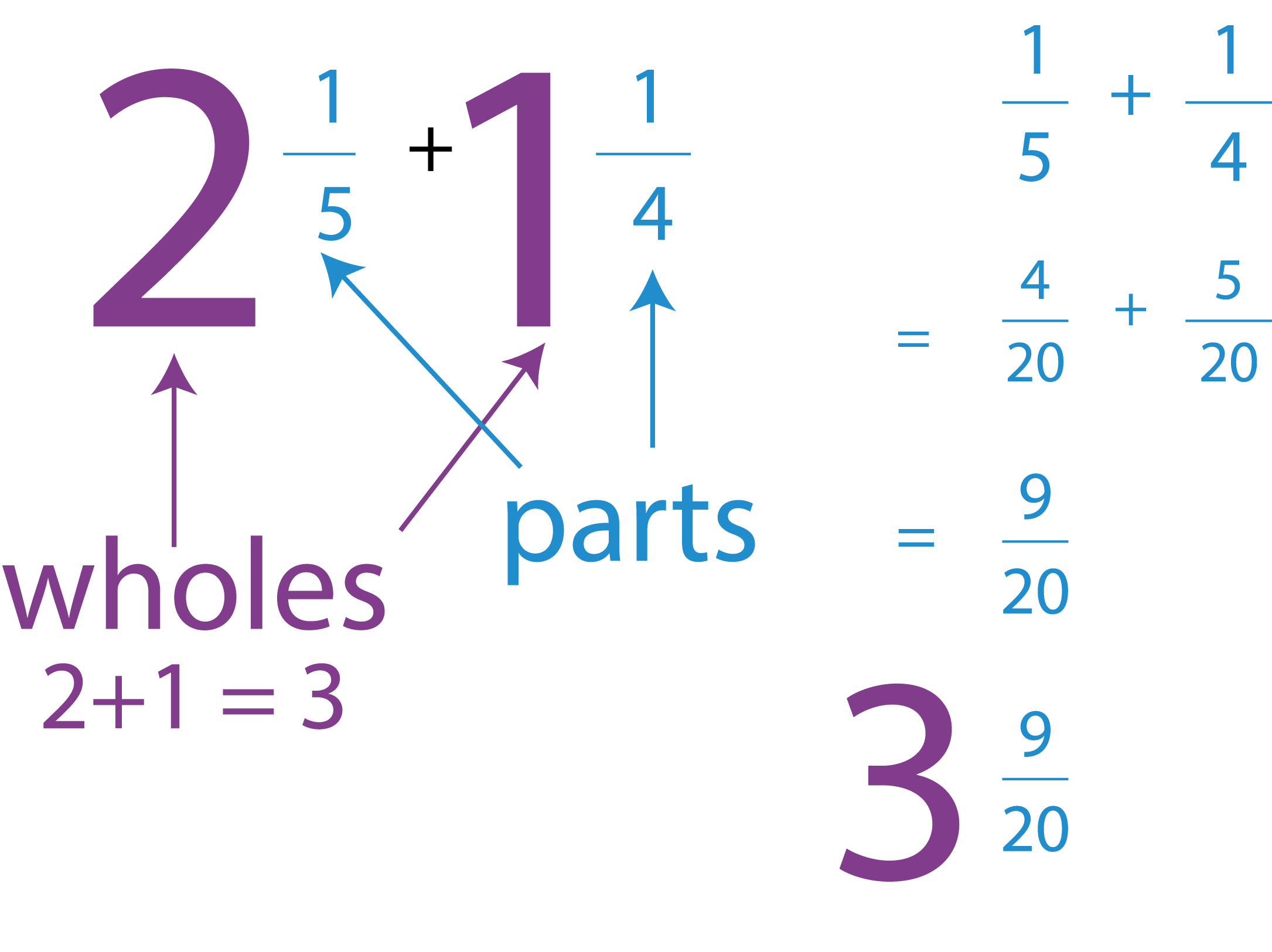
Worked Examples
QUESTION 1
Work out $9\frac{4}{19}+1\frac{3}{19}$9419+1319, leaving your answer as a mixed number.
QUESTION 2
Work out $5\frac{6}{19}-1\frac{1}{19}$5619−1119, leaving your answer as a mixed number.
QUESTION 3
Work out $8\frac{1}{6}-5\frac{2}{5}$816−525, giving your answer as a mixed number in its simplest form.