Topics
5. Rigid Transformations
topic badge
United States of AmericaVirginia
Geometry

5.03 Rotations

Lesson
Practice

Rotations

Exploration

Move the slider to create a rotating image of the figure and check the boxes to explore.

Loading interactive...
  1. What do you notice about the coordinates of the preimage and image for each angle of rotation?
  2. What do you notice about the distance segments that are the same color?
  3. What do you notice about the angles formed by the pairs of same colored segments?

A rotation is a transformation of a figure by turning it about a point called the center of rotation. The amount of rotation can be expressed in the number of degrees. The direction of the rotation for two-dimensional figures can be described in the clockwise or counterclockwise direction. When it is not specified we assume the direction is counterclockwise.

Connecting the center of rotation to any point on the pre-image and to its corresponding point on the rotated image, the line segments are equal in length and the measure of the angle formed is the angle of rotation.

-4
-3
-2
-1
1
2
3
4
x
-4
-3
-2
-1
1
2
3
4
y

When rotated about the origin, the coordinate mappings are as follows:

  • Degree of rotation counterclockwise: 90 \degree \, \, \, \qquad Coordinate mapping: \left(x,y \right) \to \left(-y,x\right)

  • Degree of rotation counterclockwise: 180 \degree \qquad Coordinate mapping: \left(x,y \right) \to \left(-x,-y\right)

  • Degree of rotation counterclockwise: 270 \degree \qquad Coordinate mapping: \left(x,y \right) \to \left(y,-x\right)

  • Degree of rotation counterclockwise: 360 \degree \qquad Coordinate mapping: \left(x,y \right) \to \left(x,y\right)

Examples

Example 1

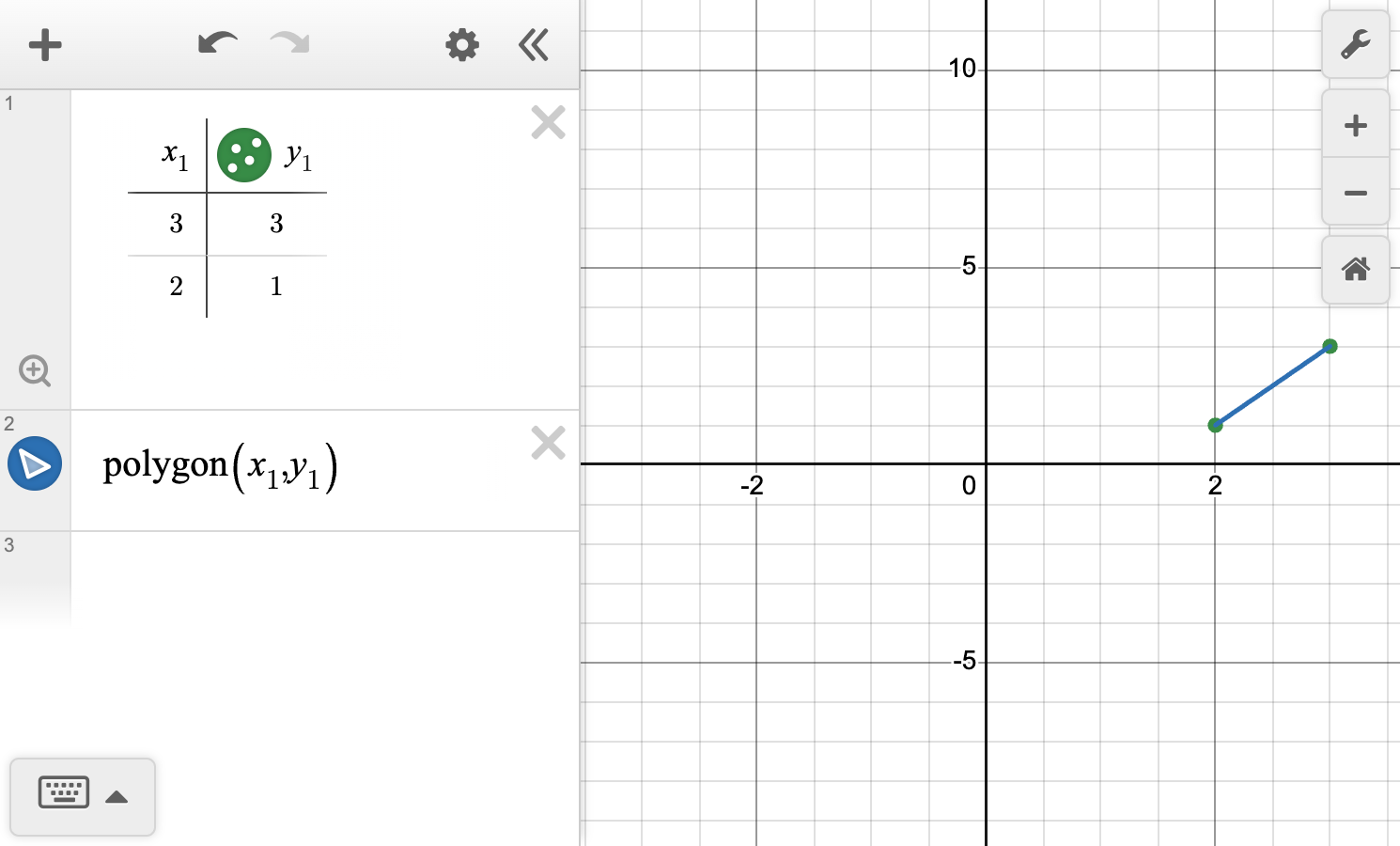
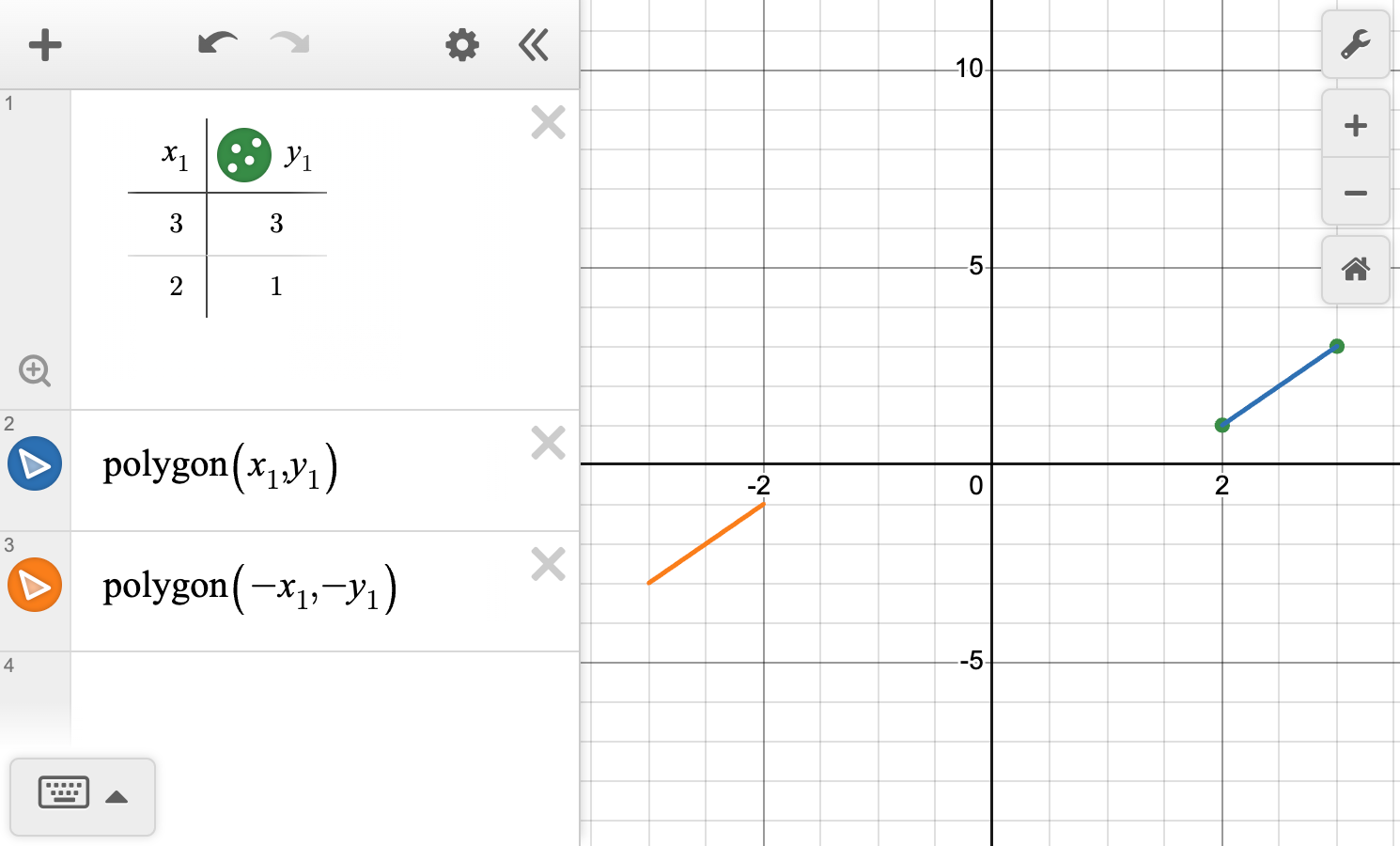
\overline{AB} has been rotated counterclockwise about the origin.

-3
-2
-1
1
2
3
x
-3
-2
-1
1
2
3
y
a

Describe the rotation required to map \overline{AB} to \overline{A'B'}.

Worked Solution
Create a strategy

We can identify the rotation that has taken place by drawing connecting segments from the origin (center of rotation), O, to point B and to point B', and then measuring the angle.

Apply the idea
-3
-2
-1
1
2
3
x
-3
-2
-1
1
2
3
y

In this case, \angle BOB' creates a straight line. The segment has been rotated 180\degree.

Reflect and check

A 180\degree rotation in the clockwise direction gives the same images as a 180\degree rotation in the counterclockwise direction. This is why we did not need to specify the direction.

b

Write the coordinate mapping.

Worked Solution
Create a strategy

We can compare the coordinates of the preimage and image to determine what the coordinate mapping looks like.

Apply the idea

We can see that A\to A' maps \left(3, 3\right) \to \left(-3,-3\right) and B\to B' maps \left(2, 1\right) \to \left(-2,-1\right). Both are of the form \left(x,y\right)\to\left(-x,-y\right) which corresponds to a 180\degree counterclockwise rotation about the origin.

Example 2

Rotate 270 \degree counterclockwise about the origin.

-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
x
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
y
Worked Solution
Create a strategy

We can determine the coordinate mapping for a rotation 270 \degree counterclockwise about the origin, then use it to find the new coordinates of quadrilateral ABCD.

Apply the idea

For 270 \degree rotation counterclockwise, the coordinate mapping is: \left(x,y\right) \to \left(y,-x\right)

-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
x
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
y

A\to A' maps (2,3) \to (3, -2)

B\to B' maps (7,3) \to (3, -7)

C\to C' maps (6,7) \to (7, -6)

D\to D' maps (3,7) \to (7, -3)

Reflect and check

We can draw connecting segments from the point of origin to points A and A', then use a protractor or technology to see if the angle formed (counterclockwise) is 270\degree.

-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
x
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
y

Notice that a rotation 90\degree clockwise about the origin is the same as a 270\degree counterclockwise rotation, so their coordinate mappings are the same.

  • 270 \degree rotation counterclockwise: Coordinate mapping: \left(x,y \right) \to \left(y,-x\right)

  • 90 \degree rotation clockwise:\\Coordinate mapping: \left(x,y \right) \to \left(y,-x\right)

Example 3

A quadrilateral undergoes a 90 \degree clockwise rotation, resulting in an image with vertices at A' \left(2, 7 \right),\, B' \left(3, 2\right),\,C' \left(8, 3\right), and D' \left(7, 8\right).

Determine the coordinates of the preimage vertices A, B, C, and D before the rotation.

Worked Solution
Create a strategy

To reverse the 90\degree clockwise rotation, we can apply the coordinate mapping for a 90\degree counterclockwise rotation.

Apply the idea

Given the coordinates of the resulting image, apply the coordinate mapping for a 90\degree counterclockwise rotation: \left(x,y\right)\to\left(-y,x\right)

  • A'\left(2,7\right) \to A\left(-7,2\right)

  • B'\left(3,2\right) \to B\left(-2,3\right)

  • C'\left(8,3\right) \to C\left(-3,8\right)

  • D'\left(7,8\right) \to D\left(-8,7\right)

Reflect and check

Plotting the coordinates of the preimage and the resulting image, then drawing a line segment from the origin to vertices A and A', we can observe that the angle formed by the rotation is 90\degree. The preimage is at the left side of the resulting image, indicating the reverse of the 90\degree clockwise rotation.

-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
y
Idea summary

When rotated counterclockwise about the origin, the transformation mappings are as follows:

  • Degree of rotation: 90 \degree \, \, \, \qquad Coordinate mapping: \left(x,y \right) \to \left(-y,x\right)

  • Degree of rotation: 180 \degree \qquad Coordinate mapping: \left(x,y \right) \to \left(-x,-y\right)

  • Degree of rotation: 270 \degree \qquad Coordinate mapping: \left(x,y \right) \to \left(y,-x\right)

  • Degree of rotation: 360 \degree \qquad Coordinate mapping: \left(x,y \right) \to \left(x,y\right)

Outcomes

G.RLT.3

The student will solve problems, including contextual problems, involving symmetry and transformation.

G.RLT.3cii

Given an image or preimage, identify the transformation or combination of transformations that has/have occurred. Transformations include: ii) reflections over any horizontal or vertical line or the lines y = x or y = -x;

G.RLT.3ciii

Given an image or preimage, identify the transformation or combination of transformations that has/have occurred. Transformations include: iii) clockwise or counterclockwise rotations of 90°, 180°, 270°, or 360° on a coordinate grid where the center of rotation is limited to the origin;

What is Mathspace

About Mathspace