6.04 Conditional probability

Conditional probability

Sometimes, probabilities need to be calculated under certain conditions. For example, what is the probability of it snowing tomorrow given the temperature today, or if an even number is rolled on a die what is the probability that it is a six. Conditions will, in effect, reduce the sample space. 

For two events $A$A and $B$B, the probability of event $A$A occurring given that event $B$B has occurred has the notation $Pr\left(A|B\right)$Pr(A|B) which is read as the "probability of $A$A given $B$B".

 

Worked examples

Example 1

What is the probability of rolling a $6$6 given that an even number has been rolled?

Let's define the two events involved, event $A$A: rolling a six and event $B$B: rolling an even number.

Since we know an even number has been rolled the possible outcomes has reduced from $\left\{1,2,3,4,5,6\right\}${1,2,3,4,5,6} to $\left\{2,4,6\right\}${2,4,6}. Of these, there is one favourable outcome which is both even and a six.

$Pr\left(A|B\right)$Pr(A|B)	$=$=	$\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes​
	$=$=	$\frac{1}{3}$13​

If we consider how we found these figures we can come up with a rule for finding $Pr\left(A|B\right)$Pr(A|B). The number of outcomes possible was reduced to be the number of outcomes for event $B$B - since this was given to have happened. The number of favourable outcomes must be in the reduced set of outcomes and match event $A$A, hence it is the number of elements in $A\cap B$A∩B.  If $n\left(X\right)$n(X)represents the number of outcomes in event $X$X, then:

$Pr\left(A|B\right)=\frac{n\left(A\cap B\right)}{n\left(B\right)}$Pr(A|B)=n(A∩B)n(B)​

Let's look at one more example using a Venn diagram.

Example 2

$56$56 students from two year 12 classes were surveyed and asked if they studied Mathematics and/or Physics. The results are shown in the Venn diagram below:

a) If a student is selected at random, what is the probability the student studies Mathematics?

This is not a conditional probability question and can be calculated using the number of students studying Mathematics and the total number of students.

$Pr\left(\text{Mathematics}\right)$Pr(Mathematics)	$=$=	$\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes​
	$=$=	$\frac{35}{56}$3556​
	$=$=	$\frac{5}{8}$58​

b) If a student is selected at random what is the probability that the student studies Mathematics given that they study Physics?

This is a conditional probability, we have been given that the student selected studies Physics. This will reduce the students we are interested in to just those studying Physics:

We now have a reduced total outcome of $25$25 students and of these, $15$15 study Mathematics.

$Pr\left(\text{Mathematics|Physics}\right)$Pr(Mathematics|Physics)	$=$=	$\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes​
	$=$=	$\frac{n\left(\text{Mathematics}\cap\text{Physics}\right)}{n\left(\text{Physics}\right)}$n(Mathematics∩Physics)n(Physics)​
	$=$=	$\frac{15}{25}$1525​
	$=$=	$\frac{3}{5}$35​

c) If a student is selected at random what is the probability that the student studies Physics given that they study Mathematics?

This is a conditional probability. We have been given that the student selected studies Mathematics. This will reduce the students we are interested in to just those studying Mathematics:

There is now a reduced total outcome of $35$35 students, and of these $15$15 study Physics.

$Pr\left(\text{Physics|Mathematics}\right)$Pr(Physics|Mathematics)	$=$=	$\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes​
	$=$=	$\frac{n\left(\text{Physics}\cap\text{Mathematics}\right)}{n\left(\text{Mathematics}\right)}$n(Physics∩Mathematics)n(Mathematics)​
	$=$=	$\frac{15}{35}$1535​
	$=$=	$\frac{3}{7}$37​

Notice in our example $Pr\left(A|B\right)\ne Pr\left(B|A\right)$Pr(A|B)≠Pr(B|A) and this is true in general. Can you see under what conditions they would be equal?

The probability of event A occurring given event B has occurred can be calculated using:

$Pr\left(A|B\right)=\frac{n\left(A\cap B\right)}{n\left(B\right)}$Pr(A|B)=n(A∩B)n(B)​

Dividing the top and bottom terms of this fraction by the total number of outcomes, each term would be expressible as a probability. This allows for the calculation of conditional probabilities using the probabilities of events rather than the number of outcomes.

Note: A Venn diagram may be expressed in terms of the number of elements in each section or, by dividing by the total number of outcomes, it's possible to create equivalent Venn diagrams displaying the probabilities of each section. For example, if 40 people were surveyed and asked if they own a pet dog and/or cat, this information could be represented as either diagram below. 

Worked example

Example 3

Use the probability Venn diagram below to calculate the following probabilities.

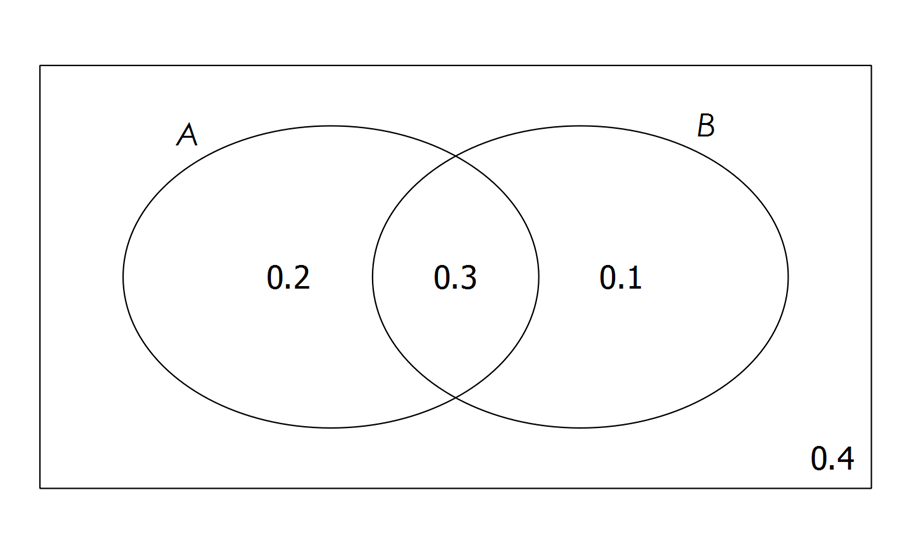
a)  $Pr(A|B)$Pr(A|B)

$Pr\left(A|B\right)$Pr(A|B)	$=$=	$\frac{Pr\left(A\cap B\right)}{Pr\left(B\right)}$Pr(A∩B)Pr(B)​
	$=$=	$\frac{0.3}{0.1+0.3}$0.30.1+0.3​
	$=$=	$\frac{3}{4}$34​

b)  $Pr(B|A')$Pr(B|A′) 

$Pr\left(B|A'\right)$Pr(B|A′)	$=$=	$\frac{Pr\left(B\cap A'\right)}{Pr\left(A'\right)}$Pr(B∩A′)Pr(A′)​
	$=$=	$\frac{0.1}{0.1+0.4}$0.10.1+0.4​
	$=$=	$\frac{1}{5}$15​

 

Independent events

Recall that independent events are events where the occurrence of one event does not affect the probability of the other occurring. This would include situations such as rolling a dice and then tossing a coin, or tossing a coin repeatedly.  Now, in the context of conditional probability this would mean that the probability of event $A$A occurring given event $B$B has occurred should simply be the probability of $A$A - that is, it shouldn't matter if event $B$B occurred or not. Mathematically, this property can be written as:

$Pr\left(A|B\right)=Pr\left(A\right)$Pr(A|B)=Pr(A)

From this conditional formula, for independent events:

$Pr\left(A\cap B\right)$Pr(A∩B)	$=$=	$Pr\left(A|B\right)\times Pr\left(B\right)$Pr(A|B)×Pr(B)
	$=$=	$Pr\left(A\right)\times Pr\left(B\right)$Pr(A)×Pr(B)

This fact was used previously to calculate the probability for $Pr\left(A\cap B\right)$Pr(A∩B). Now, it is possible to use this fact to test if two events are independent if we know the probability of $A$A, $B$B and the probability of (A and B).

Dependent events

In contrast, dependent events are those events where the occurrence of one event does affect the probability of the other occurring. For example, if you select marbles from a bag full of different coloured marbles without putting the marble back after each selection, then the probability of selecting a particular colour will change depending on the colour of the marble that was previously selected and removed. The probability of being involved in a serious traffic accident is dependent on the event of driving at speed.

Our rules for conditional probabilities apply, that is: $Pr\left(A|B\right)=\frac{Pr\left(A\cap B\right)}{Pr\left(B\right)}$Pr(A|B)=Pr(A∩B)Pr(B)​

Common problems involve repeated selections from a set, such as repeated selections of cards from a deck or repeated selections of marbles from a bag or repeated selections of people from a population to form a sample. Look for the phrases with replacement or without replacement.

• With replacement means repeated selections will retain the same probability and hence, the events remain independent
• Without replacement means that the probabilities will change as a selection is made and removed as a possibility for future selections and hence, the events are dependent 
• If a population is large enough, for example selecting ten people randomly from the Australian electoral role then this case can be treated as independent since the probabilities will change so little it will not significantly affect the calculation

 

Worked examples

Example 4

Three cards are chosen at random from a deck of $52$52 cards without replacement. What is the probability of choosing $3$3 kings?

On the first draw we have $52$52 cards, and there are $4$4 kings in the pack.

On the second draw, if we have already kept a king out - then we have $51$51 cards, and $3$3 kings still in the pack.

On the third draw, because we have already kept two kings out, then we have $50$50 cards and just $2$2 kings still in the pack.  

This results in the following probability of $3$3 kings being selected:

$Pr\left(\text{3 Kings}\right)$Pr(3 Kings)	$=$=	$\frac{4}{52}\times\frac{3}{51}\times\frac{2}{50}$452​×351​×250​
	$=$=	$\frac{1}{5525}$15525​

When you solve problems like this, you may find it helpful to draw 3 boxes marking the cards you are interested in, then writing the probabilities in each box. It's then easier to see what you need to multiply to calculate the answer.

Example 5

What is the probability of drawing (without replacement) a Jack, Queen and King:

a) in that order?

b) in any order?

a)  A Jack first, well there are $4$4 possible Jacks out of $52$52 cards.

A queen next, there are $4$4 possible queens out of $51$51 cards (remember we kept out a card).

A king next, there are $4$4 possible kings out of $50$50 cards remaining.

$Pr\left(\text{J,Q,K}\right)=$Pr(J,Q,K)= $\frac{4}{52}\times\frac{4}{51}\times\frac{4}{50}=\frac{8}{16575}$452​×451​×450​=816575​

 

b) For the first card we want either a J, Q or K ($12$12 possible cards) from a total of $52$52.

For the second card, we want one of the other values ($8$8 possible cards) from a total of $51$51. For example, if the first card was a Jack, then we want any of the Kings or Queens.

For the third card we want the last card to complete the set, $4$4 possibilities from a total of $50$50 cards.

$Pr\left(\text{J,Q,K in any order}\right)=$Pr(J,Q,K in any order)= $\frac{12}{52}\times\frac{8}{51}\times\frac{4}{50}=\frac{16}{5525}$1252​×851​×450​=165525​

 

Tree Diagrams

Tree diagrams are often used to display conditional events and carry out probability calculations.

Consider the following two examples, one with replacement and one without replacement, to compare the information displayed in a tree diagram.

Worked example

Example 6

a) Draw a tree diagram to represent drawing two marbles from a bag containing $4$4 blue marble and $2$2 red marbles with replacement and find the probabilities of each outcome.

b) Draw a tree diagram to represent drawing two marbles from a bag containing $4$4 blue marble and $2$2 red marbles without replacement and find the probabilities of each outcome.

Just as for tree diagrams with replacement, we can find probabilities by multiplying across branches. The difference here is the probabilities for the second draw. The denominator has reduced to $5$5, reflecting that there are now only $5$5 marbles left in the bag and the numerator changes depending on the first draw. Take care when creating this type of tree diagram and check that the probabilities across branches originating from the same point add to $1$1.

The probabilities on the branches for draw two are in fact conditional probabilities. For example, the probability of a red on the second draw given a blue on the first is $\frac{2}{5}$25​.

The probabilities on tree diagrams for dependent events like part b) above are:

The probabilities on tree diagrams for independent events like part a) above will simplify to:

 

The tree diagram for dependent events also leads to the law of total probability for two events:

In the tree diagram, if we were interested in the probability of the second event $B$B occurring, this outcome is found in two branches: the first branch $Pr\left(B|A\right)\times Pr\left(A\right)$Pr(B|A)×Pr(A), and the third branch $Pr\left(B|A'\right)\times Pr\left(A'\right)$Pr(B|A′)×Pr(A′). The total probability for event $B$B is then:

$Pr\left(B\right)=Pr\left(B|A\right)\times Pr\left(A\right)+Pr\left(B|A'\right)\times Pr\left(A'\right)$Pr(B)=Pr(B|A)×Pr(A)+Pr(B|A′)×Pr(A′)

which is the equivalent of the rule above but with $A$A and $B$B swapped.

 

Practice questions

Question 1

QUESTION 2

QUESTION 3

QUESTION 4