Enlargements
A shape is considered an enlargement of another if each side of the first shape is multiplied by the same scale factor to form the sides of the second shape.
For example, consider a triangle with side lengths measuring $3$3 cm, $4$4 cm and $5$5 cm. If each side is multiplied by the same factor, say $2$2, the new resulting triangle will have side lengths measuring $6$6 cm, $8$8 cm and $10$10 cm. The resulting shape is larger.
Reductions
A shape is considered a reduction of another if each side of the first shape is divided by the same scale factor to form the sides of the second shape.
Consider the reverse of the above example–a triangle with side lengths measuring $6$6 cm, $8$8 cm and $10$10 cm has each side multiplied by a factor of $\frac{1}{2}$12. The new resulting triangle will have side lengths measuring $3$3 cm, $4$4 cm and $5$5 cm. The resulting shape is smaller than the original.
The scale factor tells us by how much the object has been enlarged or reduced.
$\text{linear scale factor, k}=\frac{\text{length of image}}{\text{length of object}}$linear scale factor, k=length of imagelength of object
If the scale factor is greater than $1$1, then the image is bigger than the original.
If the scale factor is less than $1$1, then the image is smaller than the original.
Worked examples
Example 1
The shape $ABCD$ABCD has been enlarged to $A'B'C'D'$A′B′C′D′. Find the scale factor.
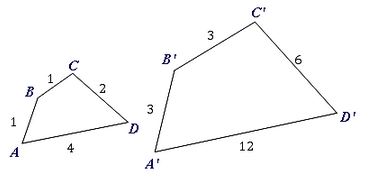
Think: To find the scale factor we want to identify corresponding sides. In some cases this might mean rotating the shape. Then we want to look for a common ratio.
Do:
| Side | Length | Side | Length | Scale factor |
|---|---|---|---|---|
| $AD$AD | $4$4 | $A'D'$A′D′ | $12$12 | $\frac{12}{4}=3$124=3 |
| $DC$DC | $2$2 | $D'C'$D′C′ | $6$6 | $\frac{6}{2}=3$62=3 |
| $CB$CB | $1$1 | $C'B'$C′B′ | $3$3 | $\frac{3}{1}=3$31=3 |
| $BA$BA | $1$1 | $B'A'$B′A′ | $3$3 | $\frac{3}{1}=3$31=3 |
Shape $A'B'C'D'$A′B′C′D′ has all side lengths $3$3 times larger than the corresponding sides of shape $ABCD$ABCD so the shapes are similar with a scale factor of $3$3.
Example 2
Are shapes $ABCD$ABCD and $SPQR$SPQR similar?
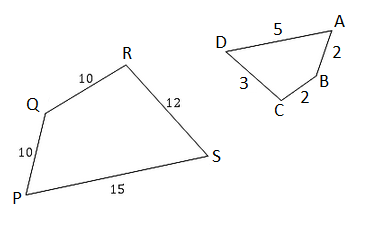
Think: Firstly, identify corresponding sides. To do this rotate $SPQR$SPQR.

Do: Now list the pairs of corresponding sides.
| Side | Length | Side | Length | Scale factor |
|---|---|---|---|---|
| $AB$AB | $2$2 | $PQ$PQ | $10$10 | $\frac{10}{2}=5$102=5 |
| $BC$BC | $2$2 | $QR$QR | $10$10 | $\frac{10}{2}=5$102=5 |
| $CD$CD | $3$3 | $RS$RS | $12$12 | $\frac{12}{3}=4$123=4 |
| $DA$DA | $5$5 | $SP$SP | $15$15 | $\frac{15}{5}=3$155=3 |
As not all the sides have been decreased by the same scale, so $ABCD$ABCD is not similar to $PQRS$PQRS.
Example 3
Another place that enlargements/reductions are used is in scale drawings. Consider this image of a plan of a tower. If we know that the actual tower is $324$324 m tall, and on this image the tower is $23.5$23.5 cm, what is the scale factor?

Think: To identify the scale factor, we want to divide the height of the actual tower by the height of the plan.
Do: Remember to convert one of the heights so that they share the same units.
| $\text{Scale factor }$Scale factor | $=$= | $\frac{\text{height of actual }}{\text{height of plan }}$height of actual height of plan |
| $=$= | $\frac{324\times100}{23.5}$324×10023.5 | |
| $=$= | $\frac{32400}{23.5}$3240023.5 | |
| $=$= | $1378.7234$1378.7234 |
So the actual tower is $1378.72$1378.72 times the height of the image on the paper.
We would write this as a scale of $1$1 cm$:$: $1378.72$1378.72 cm.
Practice questions
Question 1
Which of these shapes are enlargements of each other?
 A
A B
B C
C D
D
Question 2
Triangle A'B'C' has been reduced to form a smaller triangle ABC. What is the scale factor?

$\frac{1}{4}$14
A$3$3
B$\frac{1}{3}$13
C$4$4
D
Area scale factor
Suppose we have a square with side lengths $2$2 cm and we enlarge each side length by a scale factor of $3$3.

Lengths have been scaled by a factor $3$3, but the area has gone from $4$4 cm2 to $36$36 cm2. The area has been scaled by a factor of $9$9.
Areas of similar figures do not scale by the same factor as the scale factor of the length, and for this reason, they have their own scale factor called the area scale factor.
If enlarging or shrinking any figure, no matter how irregular, by a length scale factor of $k$k, the areas of all these squares inside it will each scale by a factor of $k^2$k2.

For any figure that is scaled by a length scale factor of $k$k, the area scale factor will be $k^2$k2.
Practice question
Question 3
Find the value of $x$x in each of the following cases:

Two rectangles. The larger rectangle, situated on the left, has a length of $27$27 cm with an area labeled as $324$324 $cm^2$cm2. The smaller rectangle, placed on the right, has a length of $9$9 cm and an area denoted as $x$x $cm^2$cm2. The widths of the rectangles are not provided in the image. 
Two hexagons. The larger hexagon on the left has bottom side measuring $21$21 cm, and its area is x $cm^2$cm2. The smaller hexagon on the right has bottom side measuring $7$7 cm, and its area is given as $56$56 $cm^2$cm2. The other dimensions of the hexagons are not specified.
Volume scale factor
Given a cube of side length $a$a units, its volume would be $a^3$a3 units3.

If scaling any figure, no matter how irregular, by a length scale factor of $k$k, the volumes of all these cubes inside it will each scale by a factor of $k^3$k3.
For any figure that is scaled by a length scale factor of $k$k, the volume scale factor will be $k^3$k3.
Practice question
Question 4
Consider the two similar trapezoidal prisms.

Find the length scale factor, going from the smaller prism to the larger prism.
Find the volume scale factor, going from the smaller prism to the larger prism.
