Prisms
A prism is defined as a solid geometric figure whose two end faces are exactly the same shape, straight and parallel.
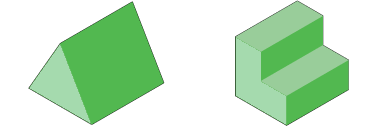
Volume of any prism
If the solid is a prism, its volume can be worked out by using the following rule.
$\text{Volume }=\text{Area of base }\times\text{Height }$Volume =Area of base ×Height
where the base is one of the two faces that are identical and parallel to one another and the height is perpendicular to the base.
In this shape, the base is the L-shaped section. It is possible to calculate the volume of an irregular prism by first calculating the area of the base and multiplying this by the height.

$\text{Volume of an irregular prism }=\text{Area of the base (L shape) }\times\text{Height of the prism }$Volume of an irregular prism =Area of the base (L shape) ×Height of the prism
$\text{Volume of rectangular prism }=\text{Length }\times\text{Width }\times\text{Height }$Volume of rectangular prism =Length ×Width ×Height
$\text{Volume of triangular prism }=\text{Area of the triangle }\times\text{Height of the prism }$Volume of triangular prism =Area of the triangle ×Height of the prism
$\text{Volume of trapezium based prism }=\text{Area of the trapezium }\times\text{Height of the prism}$Volume of trapezium based prism =Area of the trapezium ×Height of the prism
Use the following applet to experiment with how the volume of a triangular prism is affected by its base and height. You can vary the dimensions by moving the sliders and see the volume calculations by checking the checkbox.
Practice questions
Question 1
Find the volume of the cube shown.

Question 2
Find the volume of the triangular prism shown.

Question 3
Find the volume of the prism by finding the base area first.

Cylinders
A cylinder is a type of prism where the base shape is a circle.
$\text{Volume of cylinder }=\pi r^2h$Volume of cylinder =πr2h
To see how changes in height and radius affect the volume of a cylinder, try the following interactive. You can vary the height and radius by moving the sliders and view the volume calculations.
Practice questions
Question 4
Find the volume of the cylinder shown.

Round your answer to two decimal places.
Question 5
A $13$13 cm concrete cylindrical pipe has an outer radius of $6$6 cm and an inner radius of $4$4 cm as shown. Find the volume of concrete required to make the pipe, correct to two decimal places.

Exploration
You are about to go camping for the first time and need to buy a tent. You visit the local store that sells camping gear and one tent immediately attracts your attention but it appears to be a little too small for your liking. When you ask one of the salesmen for a tent with a larger volume he points you to a tent that has a similar length but double the height and that he claims is the largest tent in store. When you ask another salesman he points you to a tent that has a similar height to your original choice but double the length and that he claims is the largest tent in store. Who is right? Can they both be right?
If you think back to the formula for the volume of a triangular prism, $\frac{1}{2}\times\text{base }\times\text{height }\times\text{length of prism }$12×base ×height ×length of prism if the prism is laid out like a tent, you will notice that when the height doubles, so too will the volume; and when the length doubles, so too will the volume. So in the case of the salesmen, both of them could be right because both of the tents they point out have the same volume.
Volume of pyramids
A pyramid is formed when the vertices of a polygon are projected up to a common point (called a vertex). A right pyramid is formed when the apex is perpendicular to the midpoint of the base.

$\text{Volume of Pyramid }=\frac{1}{3}\times\text{Area of base }\times\text{Height }$Volume of Pyramid =13×Area of base ×Height
Practice questions
Question 6
Find the volume of the square pyramid shown.

Question 7
A small square pyramid of height $4$4 cm was removed from the top of a large square pyramid of height $8$8 cm forming the solid shown. Find the exact volume of the solid.

Give your answer in exact form.
Volumes of spheres
The volume of a sphere with radius $r$r can be calculated using the following formula.
$\text{Volume of sphere }=\frac{4}{3}\pi r^3$Volume of sphere =43πr3
Practice questions
Question 8
Find the volume of the sphere shown.
Round your answer to two decimal places.
Question 9
A sphere has a radius $r$r cm long and a volume of $\frac{343\pi}{3}$343π3 cm3. Find the radius of the sphere.
Round your answer to two decimal places.
Enter each line of working as an equation.
