20.03 Bearings

In surveying and air navigation, bearing are used to help identify the location of an object.

The four main directions of a compass are known as cardinal directions. They are north (N), east (E), south (S) and west (W). In between each of these cardinal direction are intermediate directions of northeast (NE), southeast (SE), southwest (SW), and northwest (NW) that are $45^\circ$45° from the two cardinal directions closest. There are smaller divisions shown on the compass as well.

Three-figure (true) bearings

A three-figure bearing are:

• measured from north ($N$N)
• measured in a clockwise direction
• written using three figures

 A $T$T is often but not always used to indicate a true bearing. If the angle measure is less than $100^\circ$100° it would be written as $040^\circ$040° or $040^\circ T$040°T.

To use true bearing to describe the location of a plane at point $B$B from the airport at point $A$A :

1. place the centre of a compass on the starting point, in the case the airport.
2. starting at North, rotate clockwise until we get to the line $AB$AB. 
3. write angle as the true bearing of point $B$B.

 

The true bearing of $B$B from $A$A is $127^\circ$127° or $127^\circ$127°$T$T.

The diagram below describes the bearing of $P$P from $O$O. Rotating clockwise from North, we get an angle of $55^\circ$55°. 

Since this measure is less than three digits, we put a 0 in front of it so the true bearing of $P$P is 055°. Consider the true bearing of $O$O from $P$P  . Since angle of elevation is equal to angle of depression and we are starting at $P$P the true bearing would be $180+55=235^\circ$180+55=235°.

 

Worked example

example 1

Find the three-figure bearing of point $P$P from $O$O.

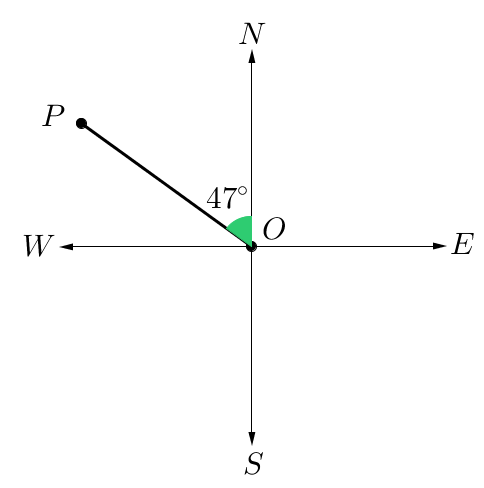
Think: To find the three-figure bearing, we want to find the measure of the angle that rotates clockwise from North to $PO$PO.

Do: Subtract the angle from $360^\circ$360°. We have $360^\circ-47^\circ=313^\circ$360°−47°=313° 

Therefore, the three-figure bearing of $P$P from $O$O is $313^\circ$313°$T$T.

 

Exploration

The bearing needed or used completely depends on which position comes first.  Have a look at the applet below. It quickly shows you how the angle changes depending on if we are measuring the bearing of $A$A from $B$B or $B$B from $A$A.

 

Practice questions

Question 1

Question 2