9.08 Constructing quadrilaterals (Investigation)

We know that a quadrilateral is a polygon with 4 sides, this means that quadrilaterals also have 4 interior angles. The other known fact we have is the the sum of the interior angles of a quadrilateral is 360\degree.

There are a number of different types of quadrilaterals, and they all have specific properties.  

Properties of quadrilaterals

 

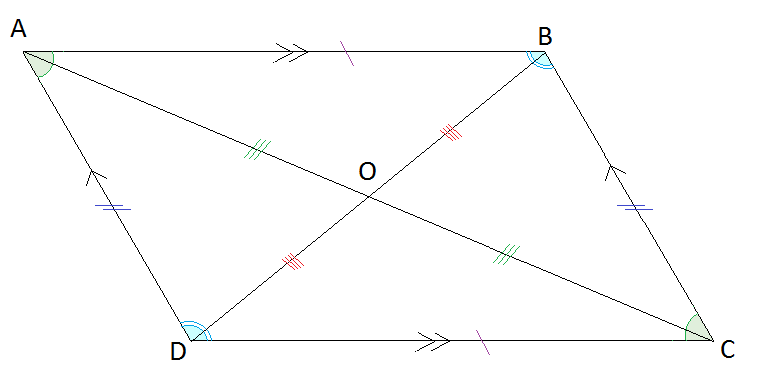
Parallelogram

• Opposite sides in a parallelogram are parallel
• Opposite angles in a parallelogram are equal
• Opposite sides in a parallelogram are equal
• Diagonals of a parallelogram bisect each other 

 

Rectangle

• Opposite sides in a rectangle are parallel
• Opposite sides in a rectangle are equal
• Diagonals of a rectangle bisect each other 
• Diagonals in a rectangle are equal 

 

Square

• All sides of a square are equal
• Opposite sides in a square are parallel
• Diagonals of a square are perpendicular to each other (cross at 90°)
• Diagonals of a square bisect the angles at the vertices (makes them 45°)
• Diagonals of a square bisect each other 
• Diagonals of a square are equal 

 

Rhombus

• Opposite angles of a rhombus are equal
• Opposite sides in a rhombus are parallel
• All sides of a rhombus are equal
• Diagonals of a rhombus bisect each other at 90 degrees 
• Diagonals of a rhombus bisect corner angles 
• Diagonals of a rhombus bisect each other

 

Trapezium

• An isosceles trapezium (trapezoid) has 2 pairs of adjacent angles equal
• A trapezium (trapezoid) has one pair of opposite sides parallel
• An isosceles trapezium (trapezoid) has one pair of opposites sides equal
• Diagonals of an isosceles trapezium (trapezoid) are equal

 

Kite

• A kite has 2 pairs of adjacent sides equal
• A kite has 1 pair of opposite angles equal
• The longest diagonal of a kite bisects the angles through which it passes 
• Diagonals of a kite are perpendicular to each other 
• The longest diagonal of a kite bisects the shorter diagonal

 

Let's explore what kind of criteria we need to be explicitly given to be able to draw a unique quadrilateral.

I'll start by asking you some questions, see if from the criteria I give you if you can draw 1, none or many quadrilaterals.

Question 1

Draw a quadrilateral with 2 sides of 4 cm, and 2 sides of 5 cm.

What kinds of quadrilaterals could you draw? How many different types?

 

Question 2

Draw a quadrilateral with with 1 pair of congruent sides, and 1 pair of parallel sides. What type is it?  Are their many different quadrilaterals that fit this criteria?

What about with 2 pairs of congruent sides and 2 pairs of parallel sides?  

• What type of quadrilateral is this one? 
• Are their many different quadrilaterals that fit this criteria?

 

Question 3

Draw a quadrilateral with 2 right angles, 1 set of parallel lines and 2 sets of perpendicular lines. 

• What type of quadrilateral is this?  
• Are there more than one type that fit this criteria?

 

Question 4

Draw a quadrilateral with no right angles and 2 sets of congruent sides of length 5 cm and 8 cm respectively.

• What type of quadrilateral is this?  
• Are there more than one type that fit this criteria?

 

Question 5

Draw a quadrilateral with no right angles, 2 pairs of parallel lines, with at least one length of exactly 5 cm.

• What type of quadrilateral is this?  
• Are there more than one type that fit this criteria?

 

Question 6

Draw a quadrilateral with no right angles, no parallel lines and no congruent lines. 

• What type of quadrilateral is this?  
• Are there more than one type that fit this criteria?

 

Question 7

Draw a quadrilateral with side lengths 3, 5, 6 and 10 cm.  

• What type of quadrilateral is this?  
• Are there more than one type that fit this criteria?