7.05 Scale factor
If we know that two figures are similar, then we know that any angle in one figure will be equal to a matching angle in the other.
Additionally, the sides opposite matching angles in the two figures will be corresponding, with the ratio between their distance being some fixed scale factor. In fact, any corresponding distances in the two figures will be in this fixed ratio.
Knowing that two figures are similar allows us to deduce information in one figure, using the given angles and sides in the other.
Matching up angles
Corresponding angles in similar figures can be easily matched up by pairing of angles of the same size. In the case where the figures have multiple angles of the same size, we can also use an angle's neighbouring angles as another requirement to be fulfilled.
For example:
In the similar figures below, both have two angles of size $98^\circ$98°.
Since the neighbouring angles of $\angle ABC$∠ABC are of sizes $126^\circ$126° and $117^\circ$117°, we know that it must correspond with $\angle PQR$∠PQR, and not with $\angle RST$∠RST.
Matching up sides
If we know which angles are corresponding in two similar figures, then the sides opposite corresponding angles will also be corresponding.
If we do not know which angles are corresponding, we can try to determine which sides are corresponding using their relative lengths.
Since each pair of corresponding sides must have their distances in the same ratio, we can use any given side lengths to determine which side lengths must be matching.
In the case where we are given all the side lengths for both similar figures, we can match up all the sides in the figures such that they all have the same ratio between their lengths.
Finding and using the scale factor
If we are given that two figures are similar and are also given two corresponding distances, we can work out the scale factor.
The scale factor is equal to a larger distance divided by the corresponding smaller distance.
The scale factor between two similar figures is the ratio of distances between the larger and smaller figure.
For example: if the distances in one similar figure are twice those of another, the scale factor between these similar figures is $2$2.
If we know the scale factor between two similar figures, then any distance in one figure can be used to calculate the corresponding distance in the other figure.
If the known distance is in the smaller figure, we can multiply by the scale factor to find the corresponding distance in the larger figure.
If the known distance is in the larger figure, we can divide by the scale factor to find the corresponding distance in the smaller figure.

In these similar figures, the scale factor is $3$3. Therefore, $x=12$x=12.
Practice questions
Question 1
The triangles in the diagram below are similar:
What is the scale factor from $\triangle ABC$△ABC to $\triangle DEF$△DEF?
Question 2
These two triangles are similar.
Find the value of $m$m.
Find the value of $n$n.
Question 3
Jenny wants to find the height of her school's flag pole. During recess, she measures the length of the flag pole's shadow to be $335$335 cm. Her friend then measures her own shadow, which turns out to be $95$95 cm.
The triangles formed by casting these shadows are similar.
If Jenny is $160$160 cm tall, what is the height of the flag pole?
Round your answer to the nearest whole centimetre.
Enlargements
A shape is considered an enlargement of another if one shape has side lengths that are all increased by the same scale factor.
Worked example
example 1
Take a triangle with side lengths measuring $3$3cm, $4$4cm and $5$5cm. If each side is multiplied by the same factor, say $2$2, the new resulting triangle will have side lengths measuring $6$6cm, $8$8cm and $10$10cm. The resulting shape is larger.
Reductions
A shape is considered a reduction of another if one shape has side lengths that are all decreased by the same scale factor.
Consider the reverse of the above example: a triangle with side lengths measuring $6$6cm, $8$8cm and $10$10cm has each side multiplied by a factor of $\frac{1}{2}$12. The new resulting triangle will have side lengths measuring $3$3cm, $4$4cm and $5$5cm. The resulting shape is smaller than the original.
The scale factor tells us by how much the object has been enlarged or reduced.
The scale factor can be greater than $1$1: the resulting image is bigger than the original.
The scale factor can be smaller than $1$1: the resulting image is smaller than the original.
Worked examples
Example 2
The shape $ABCD$ABCD has been enlarged to $A'B'C'D'$A′B′C′D′.
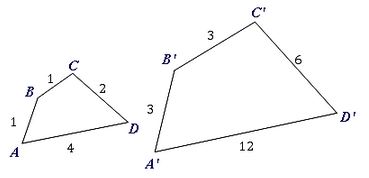
To find the scale factor we:
(a) identify corresponding sides, in some cases this might mean rotating the shape.
(b) look for a common multiple.
By aligning the largest lengths sides with each other $AD$AD and $A'D'$A′D′, and then the other sides we can set up this table.
| Side | Length | Side | Length | Scale factor |
|---|---|---|---|---|
| $AD$AD | $4$4 | $A'D'$A′D′ | $12$12 | $12\div4=3$12÷4=3 |
| $DC$DC | $2$2 | $D'C'$D′C′ | $6$6 | $6\div2=3$6÷2=3 |
| $CB$CB | $1$1 | $C'B'$C′B′ | $3$3 | $3\div1=3$3÷1=3 |
| $BA$BA | $1$1 | $B'A'$B′A′ | $3$3 | $3\div1=3$3÷1=3 |
Because shape $A'B'C'D'$A′B′C′D′ has all side lengths $3$3 times larger than the corresponding sides of shape $ABCD$ABCD we say that it has been enlarged by a factor of $3$3.
Example 3
Is shape $ABCD$ABCD an enlargement of shape $SPQR$SPQR?
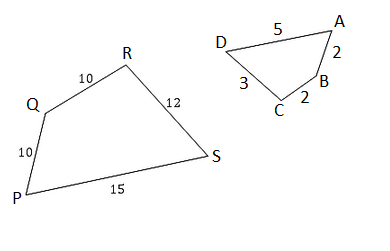
Firstly, we need to identify corresponding sides. To do this we will rotate $SPQR$SPQR.

Now we can see what might be the pairs of corresponding sides.
| SIDE | LENGTH | SIDE | LENGTH | SCALE FACTOR |
|---|---|---|---|---|
| $AB$AB | $2$2 | $PQ$PQ | $10$10 | $10\div2=5$10÷2=5 |
| $BC$BC | $2$2 | $QR$QR | $10$10 | $10\div2=5$10÷2=5 |
| $CD$CD | $3$3 | $RS$RS | $12$12 | $12\div3=4$12÷3=4 |
| $DA$DA | $5$5 | $SP$SP | $15$15 | $15\div5=3$15÷5=3 |
As not all the sides have been decreased by the same scale, the shape $ABCD$ABCD is not a reduction of $PQRS$PQRS.
Example 4
Another place that enlargements are used is in scale drawings. Consider this image of a plan of a tower. If we know that the actual tower is $324$324 m tall, and on this image the tower is $23.5$23.5 cm, we can actually deduce the scale factor.

| $\text{Scale factor }$Scale factor | $=$= | $\frac{\text{height of actual }}{\text{height of plan }}$height of actual height of plan |
| $=$= | $\frac{324m}{23.5cm}$324m23.5cm | |
| $=$= | $\frac{32400}{23.5}$3240023.5 cm | |
| $=$= | $1378.7234$1378.7234cm |
So the actual tower is $1378.72$1378.72 times the height of the image on the paper.
We would write this as a scale of $1$1cm$:$: $1378.72$1378.72cm
Practice questions
Question 4
Which of these shapes are enlargements of each other?
 A
A B
B C
C D
D
Question 5
Triangle A'B'C' has been reduced to form a smaller triangle ABC. What is the scale factor?

$\frac{1}{4}$14
A$3$3
B$\frac{1}{3}$13
C$4$4
D



