1.02 Properties of 2D shapes

Classification of 2D shapes

 

Regular

A regular polygon has all sides (and angles) equal length and size. 

These are all regular polygons.

 

Irregular

An irregular polygon has some sides (and angles) of different lengths and sizes.

These are all irregular polygons.

The word polygon comes from the Greek poly - meaning many and gonos - meaning angles.  So a polygon is a many angled figure.  

With many angles comes many sides, in fact, every 2D straight-sided shape has the same number of angles as sides.  

 

Convex or concave

Let's have a look at convex shapes first:

 

Here are some concave shapes:

 

A convex shape can be identified through two key elements:

• When drawing a line between any two vertices that the entire line is always contained inside the shape.  
• There is no angle greater than $180$180 degrees, (no reflex angles)

 

Practice question

Question 1

 

Naming 2D shapes

Different sided figures have names that describe the number of angles and sides.  

          

          

           

          

 

Sum of interior and exterior angles of 2D shapes

Angle sum of an $n$n-sided polygon is $\left(n-2\right)\times180$(n−2)×180 degrees The angles inside a quadrilateral will add up to $\left(4-2\right)\times180=360$(4−2)×180=360 degrees The angles inside a hexagon will add up to $\left(6-2\right)\times180=720$(6−2)×180=720 degrees The angles inside an octagon will add up to $\left(8-2\right)\times180=1080$(8−2)×180=1080 degrees
Sum of exterior angles of any polygon is $360^\circ$360°

 

Practice questions

Question 2

Question 3

 

Triangles

Triangles are three-sided shapes and have the following properties:

Angle sum of a triangle is $180^\circ$180°
Base angles are equal in an isosceles triangle   Sides opposite base angles are equal in an isosceles triangle
All angles in an equilateral triangles are equal   All angles in an equilateral triangle are equal to $60^\circ$60°   All sides in an equilateral triangle are equal

 

Practice question

Question 4

 

Quadrilaterals

Quadrilaterals are four-sided shapes and have the following properties:

Angle sum of a quadrilateral is $360^\circ$360°.

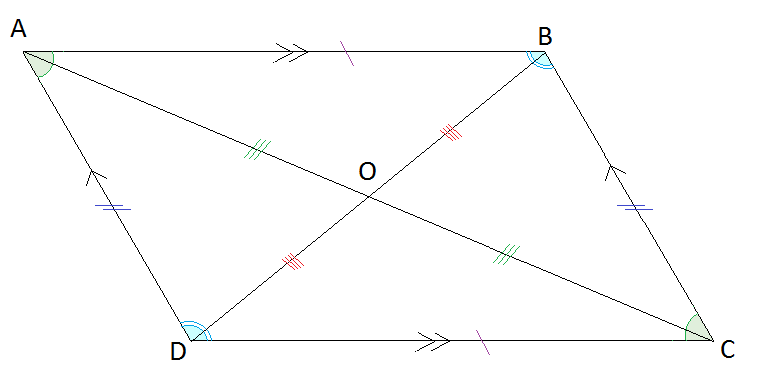
Parallelogram

• Opposite sides in a parallelogram are parallel
• Opposite angles in a parallelogram are equal
• Opposite sides in a parallelogram are equal
• Diagonals of a parallelogram bisect each other 

 

Rectangle

• Opposite sides in a rectangle are parallel
• Opposite sides in a rectangle are equal
• Diagonals of a rectangle bisect each other 
• Diagonals in a rectangle are equal 

 

Square

• All sides of a square are equal
• Opposite sides in a square are parallel
• Diagonals of a square are perpendicular to each other (cross at $90^\circ$90°)
• Diagonals of a square bisect the angles at the vertices (makes them $45^\circ$45°)
• Diagonals of a square bisect each other 
• Diagonals of a square are equal 

 

Rhombus

• Opposite angles of a rhombus are equal
• Opposite sides in a rhombus are parallel
• All sides of a rhombus are equal
• Diagonals of a rhombus are perpendicular to each other
• Diagonals of a rhombus bisect corner angles 
• Diagonals of a rhombus bisect each other

 

Trapezium

• A trapezium (trapezoid) has one pair of opposite sides parallel
• An isosceles trapezium (trapezoid) has $2$2 pairs of adjacent angles equal
• An isosceles trapezium (trapezoid) has one pair of opposites sides equal
• Diagonals of an isosceles trapezium (trapezoid) are equal

 

Kite

• A kite has $2$2 pairs of adjacent sides equal
• A kite has $1$1 pair of opposite angles equal
• The longest diagonal of a kite bisects the angles through which it passes 
• Diagonals of a kite are perpendicular to each other 
• The longest diagonal of a kite bisects the shorter diagonal

 

Practice questions

Question 5

Question 6