Speed, distance and time formulas
$\text{average speed}=\frac{\text{total distance travelled}}{\text{total time taken}}$average speed=total distance travelledtotal time taken
$S=\frac{D}{T}$S=DT
| Unknown time | Unknown distance |
|---|---|
| $T=\frac{D}{S}$T=DS | $D=S\times T$D=S×T |
Map scales
To create maps, building plans, and other technical drawings, the features being represented must be scaled down to fit on the piece of paper, and we express this scaling factor with a ratio. For example, if a small city is $100000$100000 times larger than a piece of paper, scaling its features down onto a map drawn on that paper would have the scaling ratio of $1:100000$1:100000, meaning $1$1 cm measured on the map represents $100000$100000 cm (or $1$1km) in real life.
Another way to represent the distances on a map or building plan is to use a scale bar. This small bar on the drawing shows the corresponding distance in real life. On a map, a scale bar might measure $10$10 cm long, but if it is labelled as $20$20 km we know that if two features are $10$10 cm apart on the map then they are $20$20 km apart in real life.
Practice question
Question 1
Ned took a plane from Brisbane to Townsville. The flight time was $2.4$2.4 hours. If the distance between Brisbane and Townsville is $5.8$5.8 units as it appears on the map, what is the average speed of the airplane?
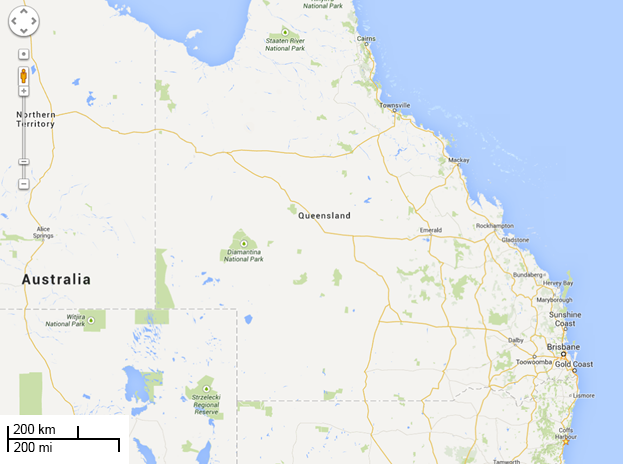
Evaluate the answer to two decimal places.