Conditional probability
We are often interested in probabilities under certain conditions. For example what is the probability of it snowing tomorrow given the condition that it is summer? Or if the condition is that an even number is rolled on a die, what is the probability that it is a six? A condition will often reduce the sample space for the problem we are concerned with.
For two events $A$A and $B$B the probability of event $A$A occurring given that event $B$B has occurred has the notation $P\left(A|B\right)$P(A|B) which is read as the "probability of $A$A given $B$B". $B$B is the condition and the number of elements in $B$B is the denominator in the probability fraction.
When considering whether a question is referring to a conditional probability, remember to look out for the following phrases:
- Given that ....
- If ......., what is the probability that .....
- The number of elements in the condition is the denominator
Worked examples
Example 1
What is the probability of rolling a $6$6 given that an even number has been rolled?
Think: Let's define the two events involved, event $A$A: rolling a six and event $B$B: rolling an even number.
Since the condition is that an even number has been rolled, the possible outcomes has reduced from $\left\{1,2,3,4,5,6\right\}${1,2,3,4,5,6} to $\left\{2,4,6\right\}${2,4,6}. Of these there is $1$1 favourable outcome which is both even and a six.
Do:
| $P\left(A|B\right)$P(A|B) | $=$= | $\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes |
| $=$= | $\frac{1}{3}$13 |
Reflect: If we consider how we found these figures we can come up with a rule for finding $P\left(A|B\right)$P(A|B). The number of outcomes possible was reduced to be the number of outcomes for event $B$B - since this was given to have happened. The number of favourable outcomes must be in the reduced set of outcomes and match event $A$A, hence it is the number of elements in $A\cap B$A∩B. If $n\left(X\right)$n(X)represents the number of outcomes in event $X$X, then:
$P\left(A|B\right)=\frac{n\left(A\cap B\right)}{n\left(B\right)}$P(A|B)=n(A∩B)n(B)
Example 2
$56$56 students from two year 12 classes were surveyed and asked if they studied Mathematics and/or Physics. The results are shown in the Venn diagram below:

(a) If a student is selected at random what is the probability the student studies Mathematics?
Think: This is not a conditional probability question and can be calculated using the number of students studying Mathematics and the total number of students.
Do:
| $P\left(\text{Mathematics}\right)$P(Mathematics) | $=$= | $\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes |
| $=$= | $\frac{35}{56}$3556 | |
| $=$= | $\frac{5}{8}$58 |
(b) If a student is selected at random what is the probability that the student studies Mathematics given that they study Physics?
Think: This is a conditional probability, we have been given that the student selected studies Physics. This will reduce the students we are interested in to just those studying Physics. We ignore all numbers in the diagram, except for those in the Physics circle.

Do: We now have a reduced total outcome of $25$25 students and of these$15$15 study Mathematics.
| $P\left(\text{Mathematics|Physics}\right)$P(Mathematics|Physics) | $=$= | $\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes |
| $=$= | $\frac{n\left(\text{Mathematics}\cap\text{Physics}\right)}{n\left(\text{Physics}\right)}$n(Mathematics∩Physics)n(Physics) | |
| $=$= | $\frac{15}{25}$1525 | |
| $=$= | $\frac{3}{5}$35 |
(c) If a student is selected at random what is the probability that the student studies Physics given that they study Mathematics?
Think: This is a conditional probability, we have been given that the student selected studies Mathematics. This will reduce the students we are interested in to just those studying Mathematics. Ignore all numbers in the problem except for those in the Mathematics circle.

Do: We now have a reduced total outcome of $35$35 students and of these $15$15 study Physics.
| $P\left(\text{Physics|Mathematics}\right)$P(Physics|Mathematics) | $=$= | $\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$Number of favourable outcomesTotal number of outcomes |
| $=$= | $\frac{n\left(\text{Physics}\cap\text{Mathematics}\right)}{n\left(\text{Mathematics}\right)}$n(Physics∩Mathematics)n(Mathematics) | |
| $=$= | $\frac{15}{35}$1535 | |
| $=$= | $\frac{3}{7}$37 |
Reflect: Notice in our example $P\left(A|B\right)\ne P\left(B|A\right)$P(A|B)≠P(B|A) and this is true in general. Can you see under what conditions they would be equal?
So we can calculate the probability of event A occurring given event B has occurred using:
$P\left(A|B\right)=\frac{n\left(A\cap B\right)}{n\left(B\right)}$P(A|B)=n(A∩B)n(B)
If we divide the top and bottom terms of this fraction by the total number of outcomes, each term would be expressible as a probability. This allows us to calculate conditional probabilities using the probabilities of events rather than the number of outcomes.
For two events $A$A and $B$B, the probability of $A$A occurring given that $B$B has occurred is given by:
$P\left(A|B\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}$P(A|B)=P(A∩B)P(B)
If we know the conditional probability we can calculate the probability of $A$A and $B$B using either:
$P\left(A\cap B\right)=P\left(A|B\right)P\left(B\right)$P(A∩B)=P(A|B)P(B) OR $P\left(A\cap B\right)=P\left(B|A\right)P\left(A\right)$P(A∩B)=P(B|A)P(A)
Note: A Venn diagram may be expressed in terms of the number of elements in each section or the probabilities of each section. For example, if we surveyed 40 people and asked if they own a pet dog and/or cat we could represent the information as either diagram below.

Worked example
Example 3
Use the probability Venn diagram below to calculate the following probabilities.
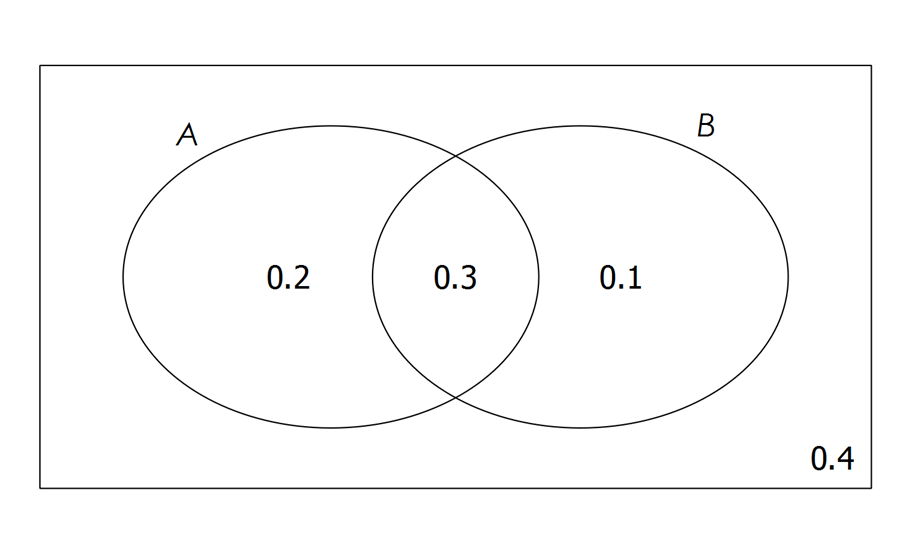
(a) $P(A|B)$P(A|B)
| $P\left(A|B\right)$P(A|B) | $=$= | $\frac{P\left(A\cap B\right)}{P\left(B\right)}$P(A∩B)P(B) |
| $=$= | $\frac{0.3}{0.1+0.3}$0.30.1+0.3 | |
| $=$= | $\frac{3}{4}$34 |
(b) $P(B|A')$P(B|A′)
| $P\left(B|A'\right)$P(B|A′) | $=$= | $\frac{P\left(B\cap A'\right)}{P\left(A'\right)}$P(B∩A′)P(A′) |
| $=$= | $\frac{0.1}{0.1+0.4}$0.10.1+0.4 | |
| $=$= | $\frac{1}{5}$15 |
Independent events
Recall that independent events are events where the occurrence of one event does not affect the probability of the other occurring. Such as rolling a dice and then tossing a coin, or tossing a coin repeatedly. Now in the context of conditional probability this would mean that the probability of event $A$A occurring given event $B$B has occurred should simply be the probability of $A$A - that is, it shouldn't matter if event $B$B occurred or not. Mathematically we can write this property as:
$P\left(A|B\right)=P\left(A\right)$P(A|B)=P(A)
From our conditional formula we see that for independent events:
| $P\left(A\cap B\right)$P(A∩B) | $=$= | $P\left(A|B\right)\times P\left(B\right)$P(A|B)×P(B) |
| $=$= | $P\left(A\right)\times P\left(B\right)$P(A)×P(B) |
We used this fact last lesson to calculate the probability for $P\left(A\cap B\right)$P(A∩B). We can now also use this fact to test if two events are independent if we know the probability of $A$A, $B$B and the probability of (A and B).
The following statements are true for any two independent events, $A$A and $B$B:
- $P\left(A\cap B\right)=P\left(A\right)\times P\left(B\right)$P(A∩B)=P(A)×P(B)
- $P\left(A|B\right)=P\left(A\right)$P(A|B)=P(A)
- $P\left(B|A\right)=P\left(B\right)$P(B|A)=P(B)
Dependent events
In contrast, dependent events are those are events where the occurrence of one event does affect the probability of the other occurring. For example, if you select marbles from a bag full of different coloured marbles without putting the marble back after each selection, then the probability of selecting a particular colour will change depending on the colour of the marble that was previously selected and removed. The probability of being involved in a serious traffic accident is dependent on the event of driving at speed.
Our rules for conditional probabilities apply, that is: $P\left(A|B\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}$P(A|B)=P(A∩B)P(B)
- $P\left(A\cap B\right)\ne P\left(A\right)\times P\left(B\right)$P(A∩B)≠P(A)×P(B)
- $P\left(A|B\right)\ne P\left(A\right)$P(A|B)≠P(A)
- $P\left(B|A\right)\ne P\left(B\right)$P(B|A)≠P(B)
Common problems involve repeated selections from a set, such as repeated selections of cards from a deck or repeated selections of marbles from a bag or repeated selections of people from a population to form a sample. Look for the phrases with replacement or without replacement.
- With replacement means repeated selections will retain the same probability and hence, the events remain independent
- Without replacement means that the probabilities will change as a selection is made and removed as a possibility for future selections and hence, the events are dependent
- If a population is large enough, for example selecting ten people randomly from the Australian electoral role then this case can be treated as independent since the probabilities will change so little it will not significantly affect the calculation
Worked examples
Example 4
Three cards are chosen at random from a deck of $52$52 cards without replacement. What is the probability of choosing $3$3 kings?
Think: On the first draw we have $52$52 cards, and there are $4$4 kings in the pack.
On the second draw, if we have already kept a king out - then we have $51$51 cards, and $3$3 kings still in the pack.
On the third draw, because we have already kept two kings out, then we have $50$50 cards and just $2$2 kings still in the pack.
Do: This results in the following probability of $3$3 kings being selected:
| $P\left(\text{3 Kings}\right)$P(3 Kings) | $=$= | $\frac{4}{52}\times\frac{3}{51}\times\frac{2}{50}$452×351×250 |
| $=$= | $\frac{1}{5525}$15525 |
Reflect: When you solve problems like this, you may find it helpful to draw a few boxes marking the 3 cards you are interested in, then writing the probabilities in each box. It's then easier to see what you need to multiply to calculate the answer.
Example 5
What is the probability of drawing (without replacement) a Jack, Queen and King:
(a) in that order?
(b) in any order?

(a) Think: A Jack first, well there are $4$4 possible Jacks out of $52$52 cards.
A queen next, there are $4$4 possible queens out of $51$51 cards (remember we kept out a card).
A king next, there are $4$4 possible kings out of $50$50 cards remaining.
Do:
$P\left(\text{J,Q,K}\right)=$P(J,Q,K)= $\frac{4}{52}\times\frac{4}{51}\times\frac{4}{50}=\frac{8}{16575}$452×451×450=816575

(b) Think: For the first card we want either a J, Q or K ($12$12 possible cards) from a total of $52$52.
For the second card, we want one of the other values ($8$8 possible cards) from a total of $51$51. For example, if the first card was a Jack, then we want any of the Kings or Queens.
For the third card we want the last card to complete the set, $4$4 possibilities from a total of $50$50 cards.
Do:
$P\left(\text{J,Q,K in any order}\right)=$P(J,Q,K in any order)= $\frac{12}{52}\times\frac{8}{51}\times\frac{4}{50}=\frac{16}{5525}$1252×851×450=165525
Tree Diagrams
Tree diagrams are often used to display conditional events and carry out probability calculations.
Let's contrast two examples: one with replacement and one without replacement to compare the information displayed in a tree diagram.
Worked example
Example 6
(a) Draw a tree diagram to represent drawing two marbles from a bag containing $4$4 blue marble and $2$2 red marbles with replacement and find the probabilities of each outcome.

(b) Draw a tree diagram to represent drawing two marbles from a bag containing $4$4 blue marble and $2$2 red marbles without replacement and find the probabilities of each outcome.

Just as for tree diagrams for with replacement, we can find probabilities by multiplying across branches. The difference here is the probabilities for the second draw. The denominator has reduced to $5$5, reflecting there are now only $5$5 marbles left in the bag and the numerator changes depending on the first draw. Take care when creating this type of tree diagram and check that the probabilities across branches originating from the same point add to $1$1.
The probabilities on the branches for draw two are in fact conditional probabilities. For example The probability of a red on the second draw given a blue on the first is $\frac{2}{5}$25.
The probabilities on tree diagrams for dependent events like part (b) above are:

The probabilities on tree diagrams for independent events like part (a) above will simplify to:

Practice questions
Question 1
Two events $A$A and $B$B are such that:
$P\left(A\cap B\right)=0.02$P(A∩B)=0.02 and $P\left(A\right)=0.2$P(A)=0.2.
If $P\left(B\right)=0.1$P(B)=0.1, are the events $A$A and $B$B independent?
Yes
ANo
BAre the events $A$A and $B$B mutually exclusive?
Yes
ANo
B
QUESTION 2
$531$531 people are asked whether they watch My Kitchen Rules ($MKR$MKR) or Masterchef ($MC$MC).
$177$177 people watch both and $65$65 watch neither. The number who watch $MKR$MKR is twice the number who watch both.
How many people only watch $MKR$MKR?
Of the people who watch $MC$MC, what proportion also watch $MKR$MKR?
Of those who don’t watch $MC$MC, what proportion watch neither?
QUESTION 3
A number game uses a basket with $9$9 balls, all labelled with numbers from $1$1 to $9$9. $3$3 balls are drawn at random, without replacement.
What is the probability that the ball labelled $3$3 is picked?
What is the probability that the ball labelled $3$3 is picked and the ball labelled $6$6 is also picked?
QUESTION 4
Sophia has three races to swim at her school swimming carnival.
The chance she wins the first one is $0.7$0.7 and if she wins, her chance of winning the second is $0.8$0.8 but if she loses then her chance of winning the second is $0.4$0.4.
If she wins the first two then her chance of winning the third is $0.9$0.9. If she lost the first two then her chance of losing the third is $0.9$0.9 and if she won only one of the first two, her chance of winning the third is $0.6$0.6.
Draw a tree diagram to represent all outcomes in this situation.
Calculate the probability Sophia won all three races.
Give your answer correct to 3 decimal places.
Calculate the probability Sophia won the third race.
Give your answer correct to 3 decimal places.
QUESTION 5
In a game of Blackjack, a player is dealt a hand of two cards from the same standard deck. What is the probability that the hand dealt:
Is a Blackjack?
(A Blackjack is an Ace paired with 10, Jack, Queen or King.)
Has a value of 20?
(10, Jack, Queen and King are all worth 10. An Ace is worth 1 or 11.)
QUESTION 6
$87$87 people are questioned about whether they own a tablet ($T$T) or a smartphone ($S$S). The probabilities shown in the list below were determined from the results.
- $P\left(T\mid S\right)=$P(T∣S)=$\frac{5}{12}$512
- $P\left(S\cap T'\right)=$P(S∩T′)=$\frac{35}{87}$3587
- $P\left(T\right)=$P(T)=$\frac{14}{29}$1429
Find the value of $n\left(S\cap T\right)$n(S∩T).
Use $Y=n\left(S\cap T\right)$Y=n(S∩T) and $X=n\left(S\cap T'\right)$X=n(S∩T′) to help you in your calculations.
Calculate $P\left(S'\cap T\right)$P(S′∩T).
Calculate $P\left(S\mid T\right)$P(S∣T).
Calculate $P\left(T\mid S'\right)$P(T∣S′).
