5.03 Circle mensuration

Recall the formulas for area and circumference of a full circle:

Arc length

What if we don't have an entire circle?  

An arc is part of the circumference of the circle. If we put any two points on a circle we will create a minor arc and a major arc.

To find the length of an arc we need to know what fraction the sector is, of a whole circle.  For this we need to know the angle of the sector.

If the angle of the sector is $\theta$θ degrees, then the fraction of the circle is represented by: 

$fraction=\frac{\theta}{360}$fraction=θ360​ (due to there being $360$360° in a circle).

Hence, the arc length can be calculated using:

$\text{Arc length}=\frac{\theta}{360^\circ}\times2\pi r$Arc length=θ360°​×2πr

What if we have the central angle in radians?

To change this to a formula for angles given in radians, we can substitute $360^\circ=2\pi$360°=2π, we get:

Arc Length	$=$=	$\frac{\theta}{2\pi}\times2\pi r$θ2π​×2πr
	$=$=	$\frac{2\pi r\theta}{2\pi}$2πrθ2π​
	$=$=	$r\theta$rθ

Often, arc length is replaced by $l$l, giving us $l=r\theta$l=rθ. This formula can also be found directly from our definition of radians as the ratio of the arc length divided by the radius. Can you see that the formula using radians is more simple to work with than if the angle was in degrees?

Sectors

A sector is a section of the circle defined by two lines from the centre to the circumference. It looks like a piece of pizza. However, there are different kinds of "slices."

A minor sector has an angle at the centre of the circle of less than $180^\circ$180°. A major sector has an angle at the centre of the circle of more than $180^\circ$180°. 

 

Perimeter of a sector

The perimeter of a sector will be the arc length plus the two radii that form the edges of the shape. Carefully read questions to determine if the perimeter or only the arc length is required.

Area of a sector

Similar to finding the length of an arc, the area of a sector is found by multiplying the area of a full circle by the appropriate fraction. 

Practice questions

QUESTION 1

QUESTION 2

QUESTION 3

Question 4

 

Area formula for non-right angled triangles

When we are using the lengths of 2 sides ($a$a and $b$b) and the angle between them $C$C.  

$\text{Area }=\frac{1}{2}\times\text{Side 1 }\times\text{Side 2 }\times\sin\theta$Area =12​×Side 1 ×Side 2 ×sinθ.  

It really doesn't matter what you call the sides as long as you have two sides and the included angle. It's worth noting that we often label the sides with lower case letters, and the angles directly opposite the sides with a capital of the same letter. The formula is most commonly written as follows:  

Practice questions

Question 4

Question 5

 

Area segments

A segment is an region formed between a chord and an arc of the circle. Each chord produces two segments: a major segment (the larger area) and the minor segment (the smaller area).

To find the area of the minor segment we can combine our knowledge of area of sectors with our recently acquired area formula for triangles ($A=\frac{1}{2}ab\sin C$A=12​absinC).

$\frac{1}{2}r^2\theta$12​r2θ		$\frac{1}{2}r^2\sin\theta$12​r2sinθ		$\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta$12​r2θ−12​r2sinθ

 

Reflect: Can you create a formula for finding the area of a segment for angles given in degrees?

How do we find the area of a major segment? In fact, the formula above will still hold. Let's see why.

The area of a major segment is just the area of the major sector, which subtends angle $\theta$θ, plus the area of a triangle with angle $2\pi-\theta$2π−θ.

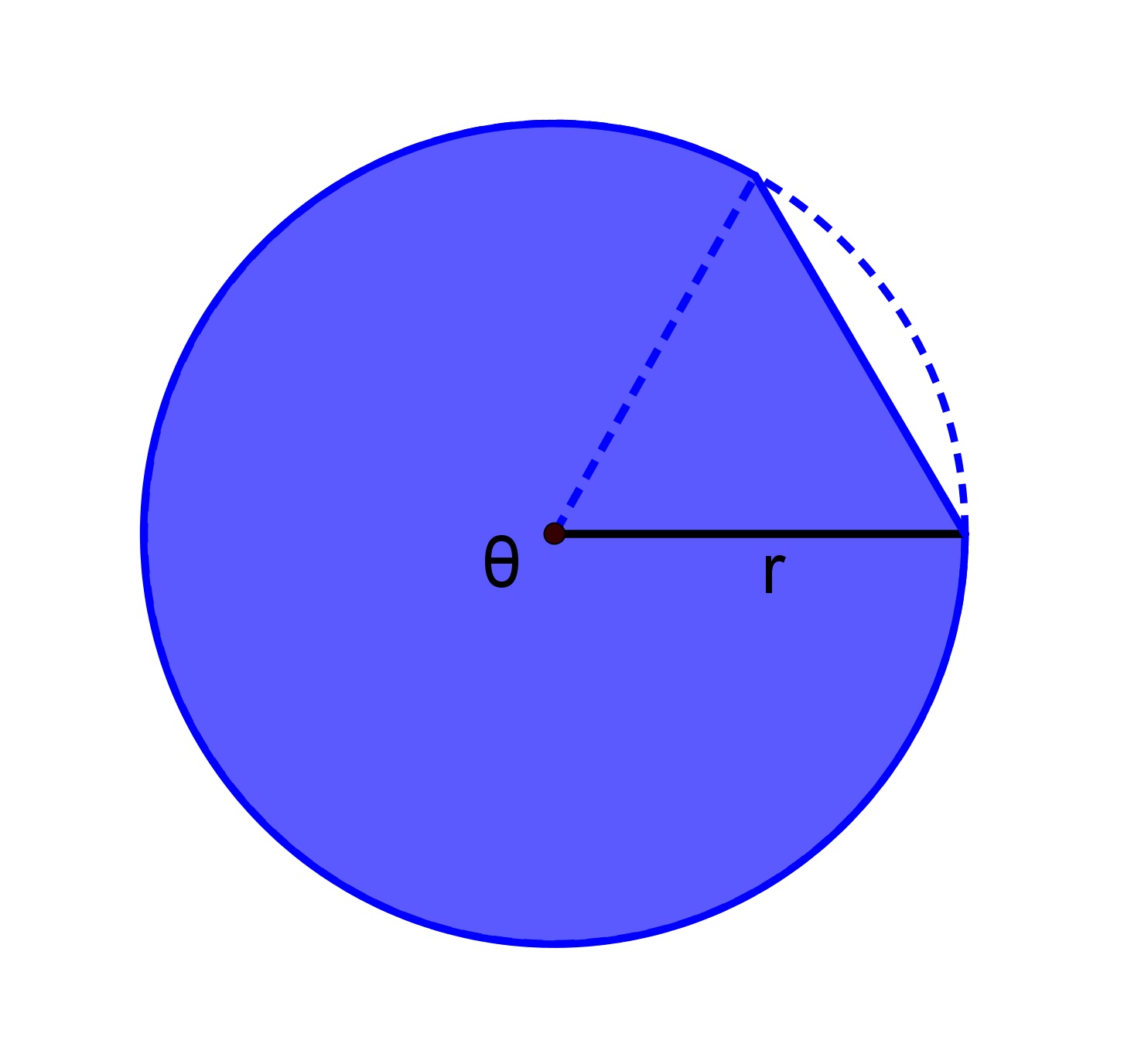$\frac{1}{2}r^2\theta$12​r2θ		$\frac{1}{2}r^2\sin\left(2\pi-\theta\right)$12​r2sin(2π−θ)		$\frac{1}{2}r^2\theta+\frac{1}{2}r^2\sin\left(2\pi-\theta\right)$12​r2θ+12​r2sin(2π−θ)

However, since $\sin\left(2\pi-\theta\right)=-\sin\theta$sin(2π−θ)=−sinθ, from the symmetry of the sine function, this is the same as our original formula:

$\text{Area of segment}$Area of segment	$=$=	$\frac{1}{2}r^2\theta+\frac{1}{2}r^2\sin\left(2\pi-\theta\right)$12​r2θ+12​r2sin(2π−θ)
	$=$=	$\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta$12​r2θ−12​r2sinθ
	$=$=	$\frac{1}{2}r^2\left(\theta-\sin\theta\right)$12​r2(θ−sinθ)

Hence, no matter what $\theta$θ is, we can use this formula to figure out the area of the segment that subtends $\theta$θ.

 

Alternatively, if we have already calculated the area of the minor segment we can subtract this from the area of the circle to find the area of the corresponding major segment.

$\pi r^2$πr2		$\frac{1}{2}r^2\left(\theta-\sin\theta\right)$12​r2(θ−sinθ)		$\pi r^2-\frac{1}{2}r^2\left(\theta-\sin\theta\right)$πr2−12​r2(θ−sinθ)

Practice questions

Question 6

Question 7

Question 8